Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Plot y=sinxa n dy=2sinxdot
Text Solution
|
- If x^m . y^n = (x+y)^(m+n) then (dy)/(dx)is:
Text Solution
|
- If x ^(n) y^(n) =( x+y ) ^(n),then (dy)/(dx)=
Text Solution
|
- If x^(n) y^(n) =(x+y) ^(n),then (dy)/(dx)=
Text Solution
|
- dy/dx + n/x y = a/x^(n)
Text Solution
|
- Plot y=sinxa n dy=sin(x/2)
Text Solution
|
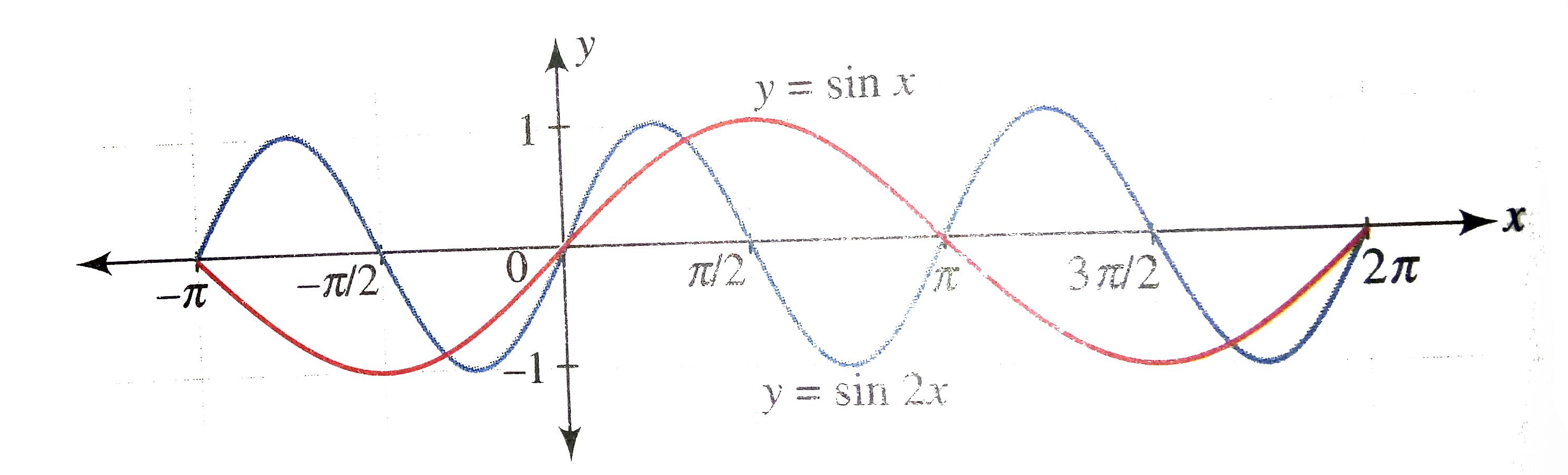
- Plot y=sinxa n dy=sin2xdot
Text Solution
|
- Plot y=sinxa n dy=sin2xdot
Text Solution
|
- Plot y=sinxa n dy=sin2xdot
Text Solution
|