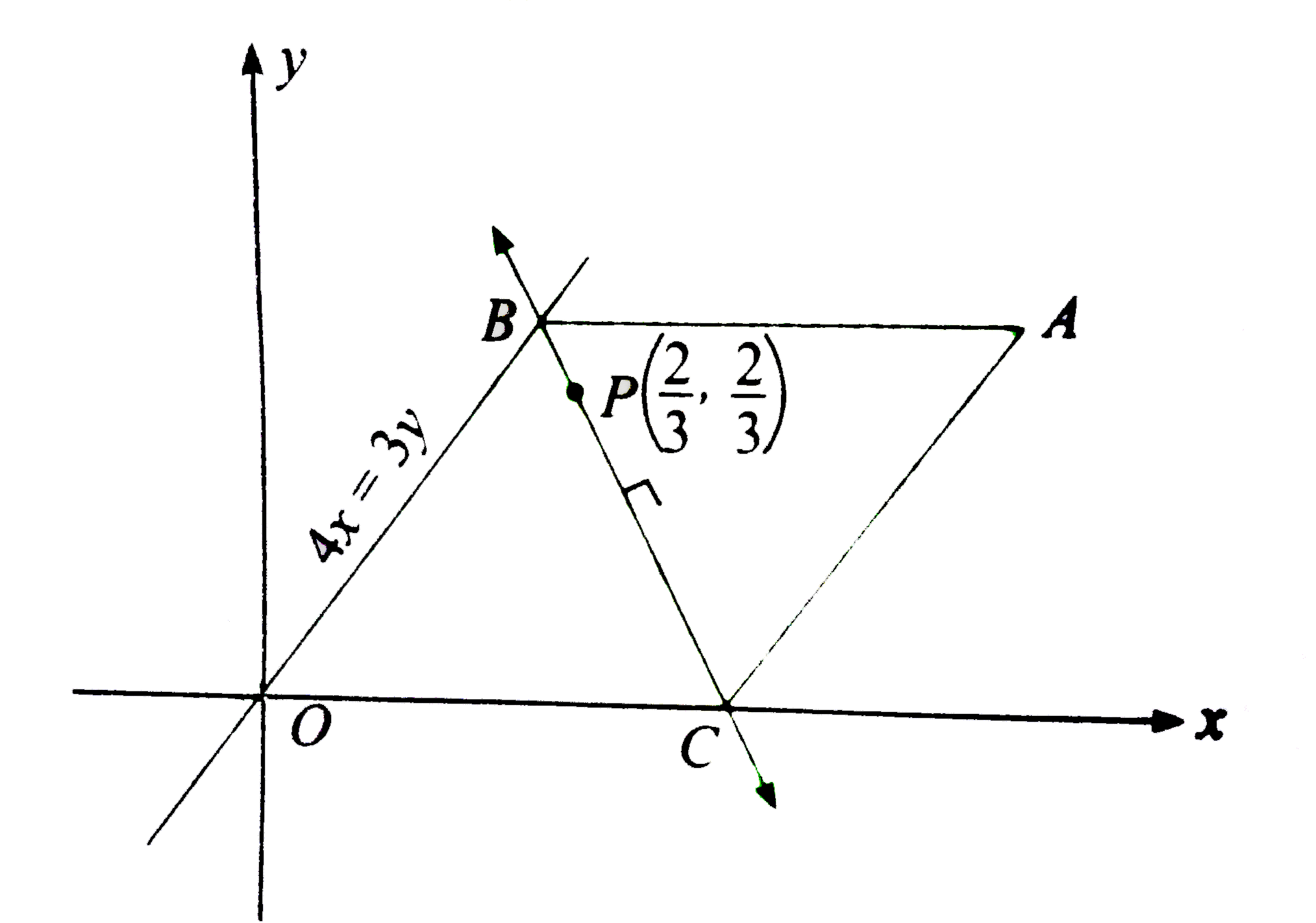Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The vertices Ba n dC of a triangle A B C lie on the lines 3y=4xa n dy=...
Text Solution
|
- The vertices Ba n dC of a triangle A B C lie on the lines 3y=4xa n dy=...
Text Solution
|
- The base of the pyramid A O B C is an equilateral triangle O B C with ...
Text Solution
|
- The vertices B and C of a triangle ABC lie on the lines 3y=4x and y=0 ...
Text Solution
|
- If sides of triangle A B C are a , ba n dc such that 2b=a+c then b/c >...
Text Solution
|
- The vertices Ba n dC of a triangle A B C lie on the lines 3y=4xa n dy=...
Text Solution
|
- The equations of the perpendicular bisectors of the sides A Ba n dA C ...
Text Solution
|
- In a triangle A B C , the bisectors of angles Ba n dC lies along the...
Text Solution
|
- The base of the pyramid A O B C is an equilateral triangle O B C with ...
Text Solution
|