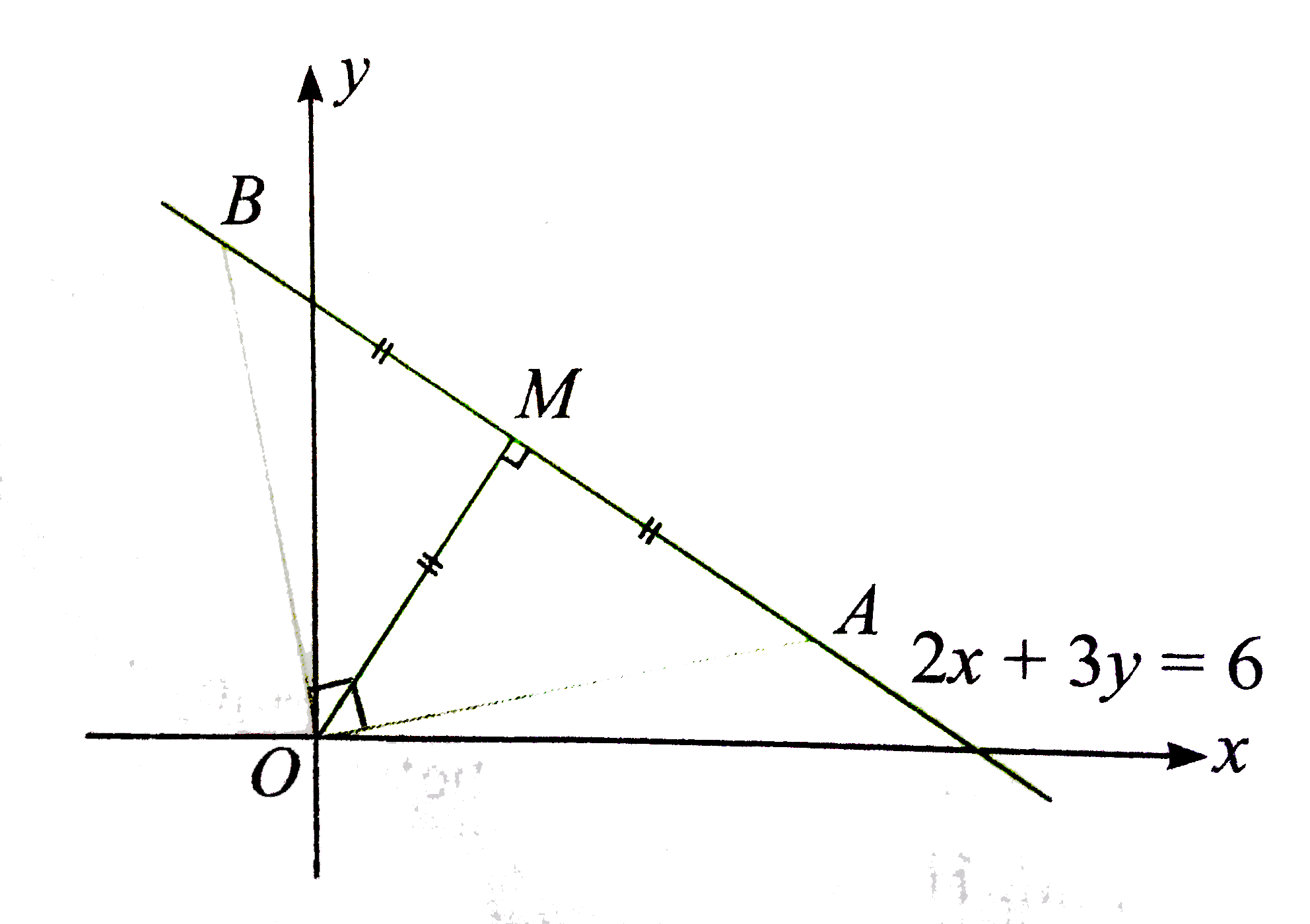
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- If a pair of perpendicular straight lines drawn through the origin ...
Text Solution
|
- If a pair of perpendicular straight lines drawn through the origin ...
Text Solution
|
- Triangle O A B is isosceles right triangle right angled at OdotO is...
Text Solution
|
- Two mutually perpendicular straight lines through the origin from an i...
Text Solution
|
- The area of the equilateral triangle formed by the lines passing throu...
Text Solution
|
- A pair of straight lines drawn through the origin form with the line ...
Text Solution
|
- Drawn from origin are two mutually perpendicular lines forming an iso...
Text Solution
|
- The equation of the pair of perpendicular lines passing through origin...
Text Solution
|
- The equation of the pair of perpendicular lines passing through o...
Text Solution
|