A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
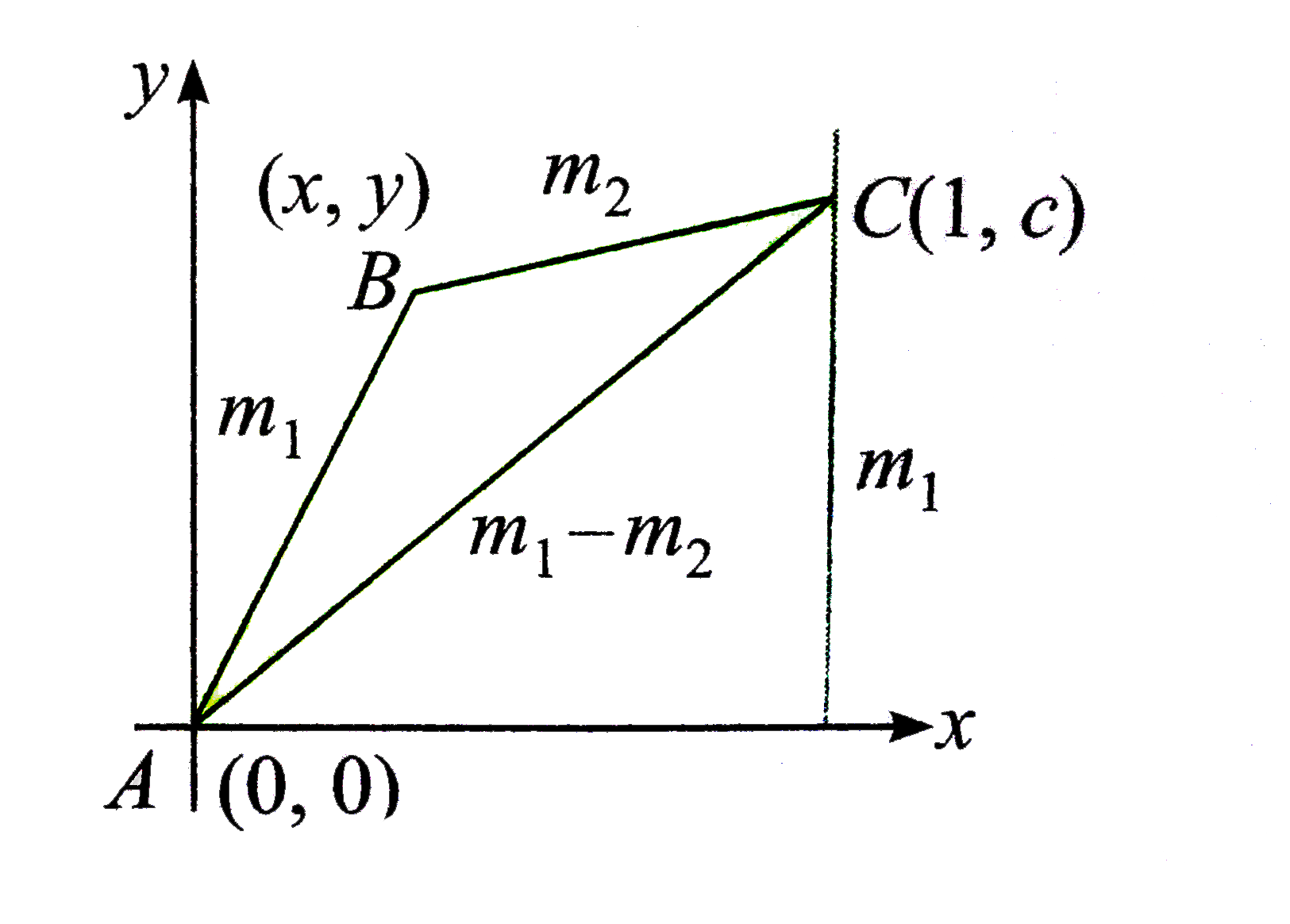
- Given A(0,0) and B(x,y) with xin(0,1) and y>0. Let the slope of line A...
Text Solution
|
- Given A(0,0) and B(x,y) with x varepsilon(0,1) and y>0. Let the slope ...
Text Solution
|
- Given A(0,0) and B(x,y) with xin(0,1) and y>0. Let the slope of line A...
Text Solution
|
- If y+3=m1(x+2) and y+3=m2(x+2) are two tangents to the parabola y2=8...
Text Solution
|
- माना एक त्रिभुज की भुजाएँ निम्न है y= m1 x+ c1 y=m2 x+c2 x=0 त...
Text Solution
|
- सिद्ध कीजिए की रेखाओं y=m1 x,y=m2 x तथा y =c द्वारा बने त्रिभुज का क्ष...
Text Solution
|
- If m1, m2(m1 > m2) are the slopes of the lines which make an angle ...
Text Solution
|
- Given A(0,0) and B(x,y) with xin(0,1) and y>0. Let the slope of line A...
Text Solution
|
- If y+3=m1(x+2) and y+3=m2(x+2) are two tangents to the parabola y2=8...
Text Solution
|