A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
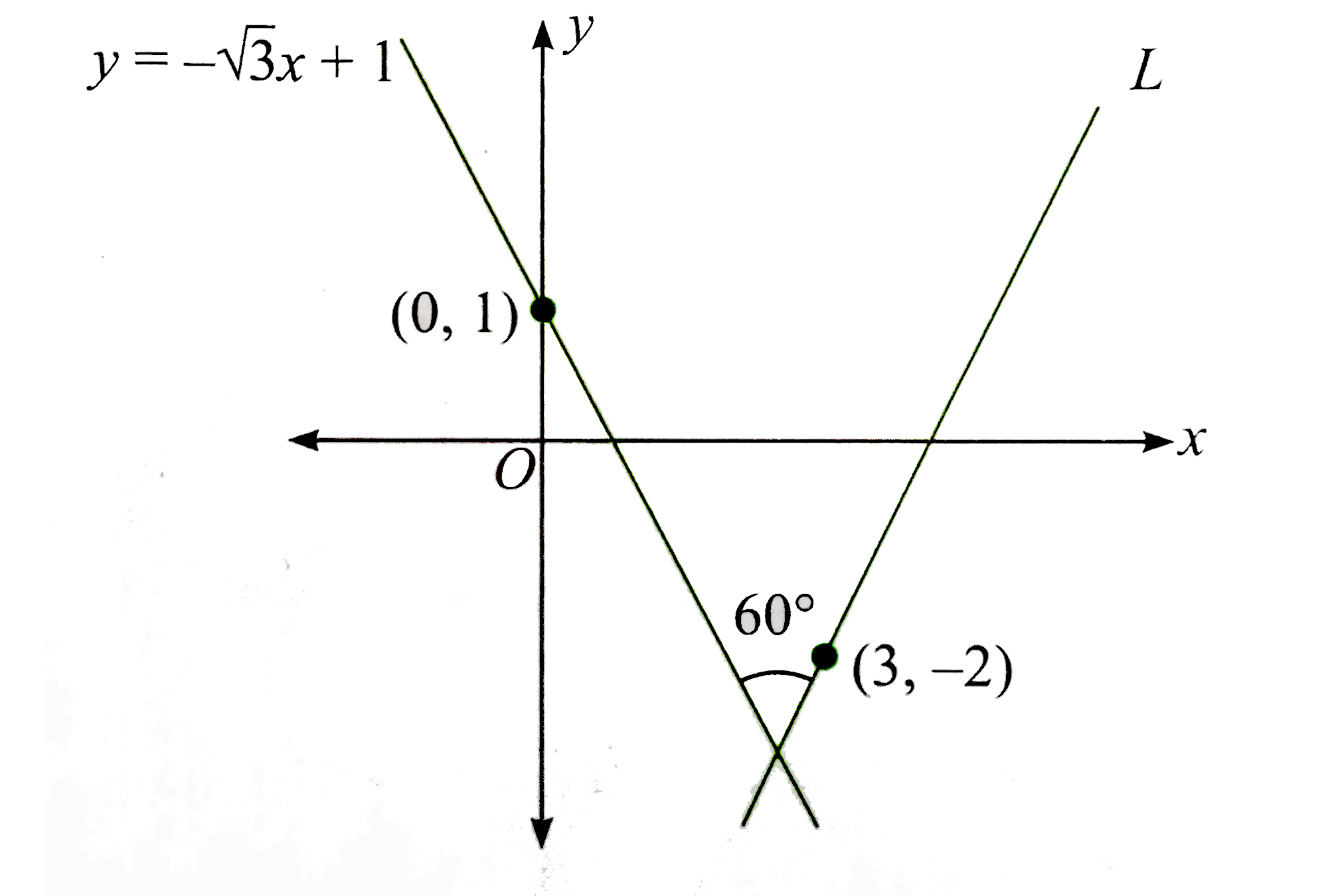
- A straight line L through the point (3,-2) is inclined at an angle 60^...
Text Solution
|
- A straight line L passes through (3,-2) also inclined at an angle 60^@...
Text Solution
|
- A straight line L through the point (3,-2) is inclined at an angle 60^...
Text Solution
|
- A straight line through the point (3, -2) is inclined at an angle 60^(...
Text Solution
|
- एक सरल रेखा L बिन्दु (3 ,-2 ) से गुजरती है और रेखा sqrt3 x +y =1 से 6...
Text Solution
|
- One of the equations of the lines passing through the point (3, -2) an...
Text Solution
|
- A straight line L through the point (3, -2) is inclined at an angle 60...
Text Solution
|
- (3,-2) বিন্দুগামী একটি সরলরেখা sqrt(3)x+y = 1 সরলরেখার সঙ্গে 60° কোণ ক...
Text Solution
|
- A straight line L through the point (3,-2) is inclined at an angle 60^...
Text Solution
|