Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
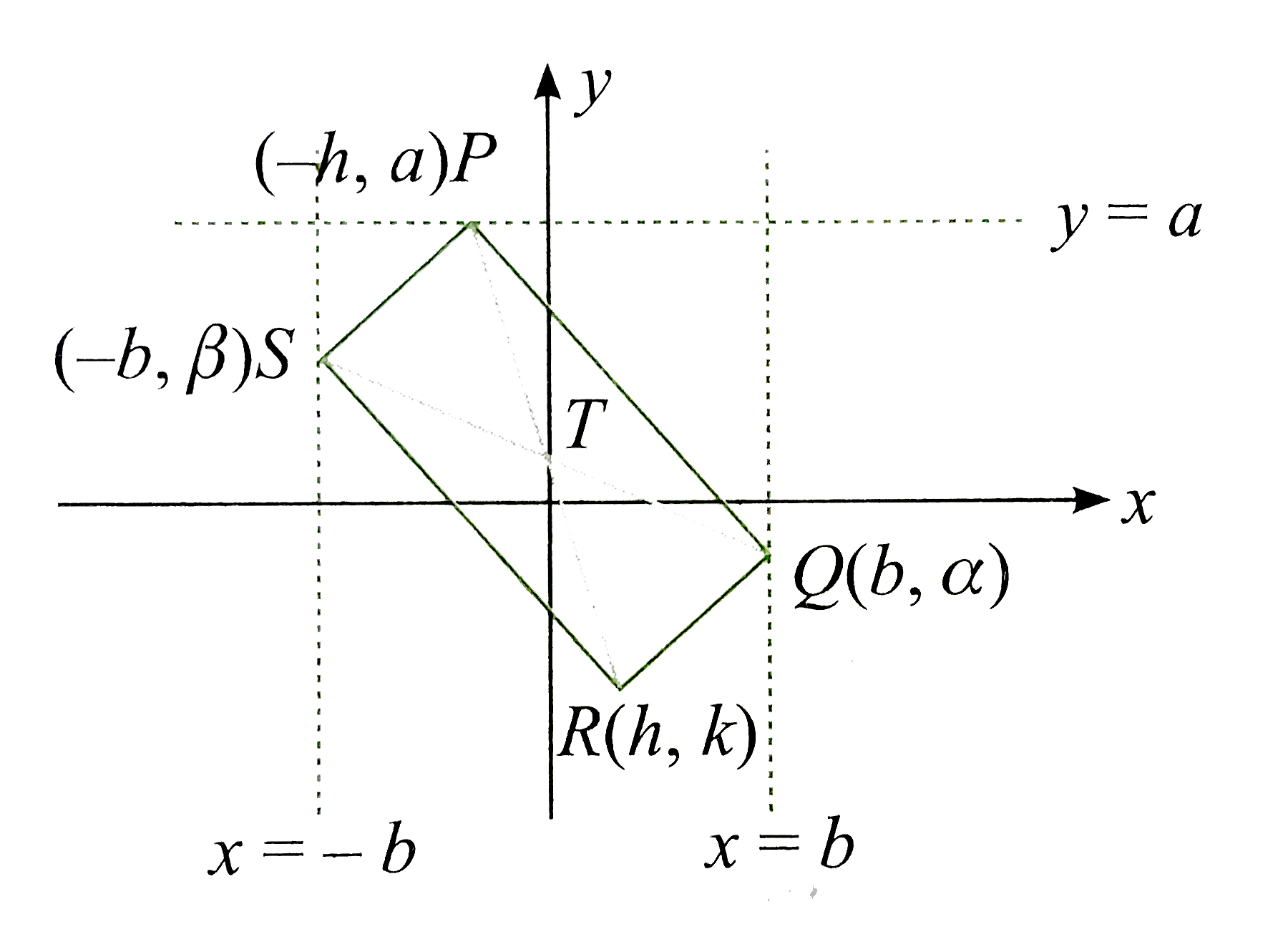
- A rectangle PQRS has its side PQ parallel to the line y= mx and verti...
Text Solution
|
- A rectangle A B C D has its side A B parallel to line y=x , and vertic...
Text Solution
|
- 42.A rectangle ABCD has its side AB parallel to the line y=x and verti...
Text Solution
|
- A rectangle PQRS has its side PQ parallel to the line y=mx and vertice...
Text Solution
|
- A rectangle PQRS has its side PQ parallel to the line y = mx and verti...
Text Solution
|
- A rectangle PQRS has its side PQ paralle to the line y=mx and vertices...
Text Solution
|
- आयत PQRS की भुजा PQ, रेखा y=mx के समान्तर है, तथा शीर्ष P, Q और ...
Text Solution
|
- एक आयत ABCD की भुजा AB, रेखा y=x के समान्तर है तथा शीर्ष A, B तथा D क्...
Text Solution
|
- A rectangle A B C D has its side A B parallel to line y=x , and vertic...
Text Solution
|