Home
Class 12
MATHS
x+y=7 and a x^2+2h x y+a y^2=0,(a!=0) , ...

`x+y=7` and `a x^2+2h x y+a y^2=0,(a!=0)` , are three real distinct lines forming a triangle. Then the triangle is (a) isosceles (b) scalene (c) equilateral (d) right angled

A

isosceles

B

scalene

C

equilateral

D

right - angled

Text Solution

Verified by Experts

The correct Answer is:
1
`ax^(2)+2hxy+ay^(2)=0`. Is symmetrical about `y=x`.
Promotional Banner

Topper's Solved these Questions

  • PAIR OF STRAIGHT LINES

    CENGAGE|Exercise Exercise (Multiple)|9 Videos

  • PAIR OF STRAIGHT LINES

    CENGAGE|Exercise Exercise (Comprehension)|6 Videos

  • PAIR OF STRAIGHT LINES

    CENGAGE|Exercise Exercise 3.2|7 Videos

  • MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS

    CENGAGE|Exercise Comprehension Type|6 Videos

  • PARABOLA

    CENGAGE|Exercise Question Bank|9 Videos

Similar Questions

Explore conceptually related problems

If all the vertices of a triangle have integral coordinates, then the triangle may be (a) right-angled (b) equilateral (c) isosceles (d) none of these

If in a triangle (1-(r_1)/(r_2))(1-(r_1)/(r_3))=2 then the triangle is right angled (b) isosceles equilateral (d) none of these

In triangle A B C ,R(b+c)=asqrt(b c),w h e r eR is the circumradius of the triangle. Then the triangle is a)isosceles but not right b)right but not isosceles c)right isosceles d)equilateral

If sinA=sin^2Ba n d2cos^2A=3cos^2B then the triangle A B C is right angled (b) obtuse angled (c)isosceles (d) equilateral

The three points (-2,2)(9,-2),a n d(-4,-3) are the vertices of (a) an isosceles triangle (b) an equilateral triangle (c) a right-angled triangle (d) none of these

If the equation 2x^2+k x y+2y^2=0 represents a pair of real and distinct lines, then find the values of kdot

The orthocenter of the triangle formed by the lines xy=0 and x+y=1 is

Show that the straight line x^2-4xy+y^2=0 and x + y = 3 form an equilateral triangle.

Show that the common tangents to the parabola y^2=4x and the circle x^2+y^2+2x=0 form an equilateral triangle.

CENGAGE-PAIR OF STRAIGHT LINES-Exercise (Single)
  1. The equation x-y=4 and x^2+4xy+y^2=0 represent the sides of

    Text Solution

    |

  2. The straight lines represented by (y-m x)^2=a^2(1+m^2) and (y-n x)^2=a...

    Text Solution

    |

  3. If the pairs of lines x^2+2x y+a y^2=0 and a x^2+2x y+y^2=0 have exact...

    Text Solution

    |

  4. The condition that one of the straight lines given by the equation a x...

    Text Solution

    |

  5. If the represented by the equation 3y^2-x^2+2sqrt(3)x-3=0 are rotated ...

    Text Solution

    |

  6. The equation of a line which is parallel to the line common to the pai...

    Text Solution

    |

  7. The equation x^(2)y^(2)-9y^(2)-6x^(2)y+54y=0 represents

    Text Solution

    |

  8. The equation a^2x^2+2h(a+b)x y+b^2y^2=0 and a x^2+2h x y+b y^2=0 repre...

    Text Solution

    |

  9. If the equation of the pair of straight lines passing through the poin...

    Text Solution

    |

  10. If two lines represented by x^4+x^3y+c x^2y^2-x y^3+y^4=0 bisect the a...

    Text Solution

    |

  11. Through a point A on the x-axis, a straight line is drawn parallel to ...

    Text Solution

    |

  12. The image of the pair of lines represented by a x^2+2h x y+b y^2=0 by ...

    Text Solution

    |

  13. The straight lines represented by the equation 135 x^2-136 x y+33 y^2=...

    Text Solution

    |

  14. If the slope of one of the lines represented by a x^2+2h x y+b y^2=0 i...

    Text Solution

    |

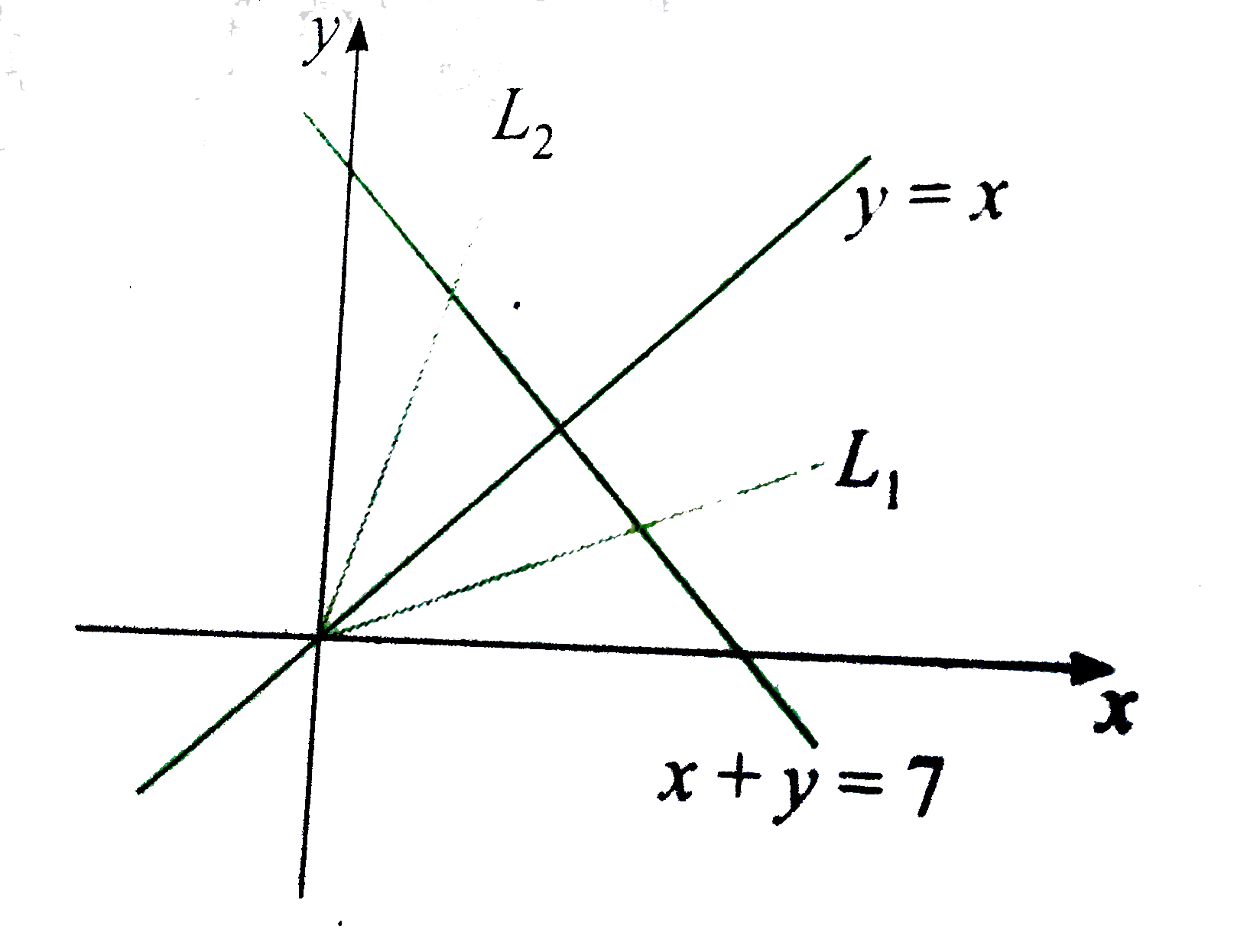
  15. x+y=7 and a x^2+2h x y+a y^2=0,(a!=0) , are three real distinct lines ...

    Text Solution

    |

  16. Statement 1 : If -h2=a+b , then one line of the pair of lines a x^2...

    Text Solution

    |

  17. The orthocenter of the triangle formed by the lines xy=0 and x+y=1 is

    Text Solution

    |

  18. Let P Q R be a right-angled isosceles triangle, right angled at P(2,1)...

    Text Solution

    |

  19. Area of the triangle formed by the line x+y=3 and the angle bisectors ...

    Text Solution

    |

  20. The orthocentre of the triangle formed by the lines 2x^(2)+3xy-2y^(2)...

    Text Solution

    |