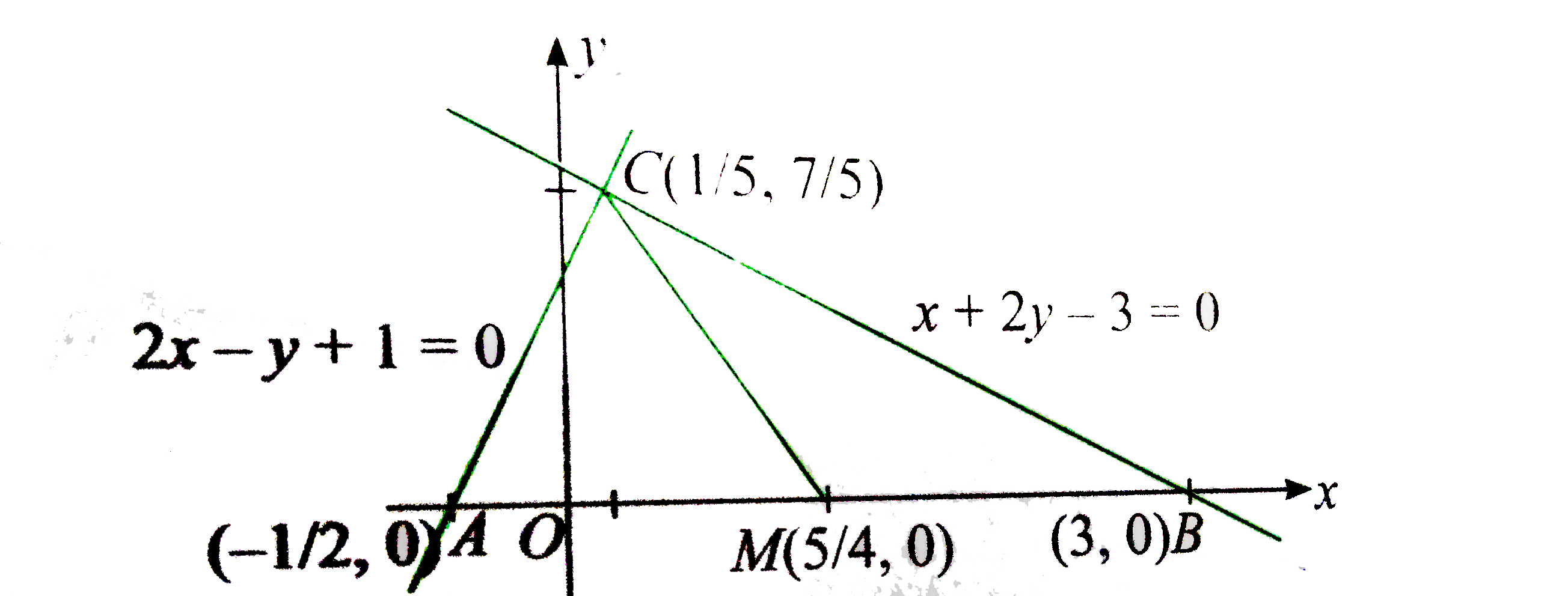A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-PAIR OF STRAIGHT LINES-Exercise (Comprehension)
- If lambdax^(2)-10xy+12y^(2)+5x-16y-3=0, represents a pair of straight ...
Text Solution
|
- Consider the equation of a pair of straight lines as lambdax^(2)-10xy+...
Text Solution
|
- Consider the equation of a pair of straight lines as lambdax^(2)-10xy+...
Text Solution
|
- Consider a pair of perpendicular straight lines ax^(2)+3xy-2y^(2)-5x+5...
Text Solution
|
- Consider a pair of perpendicular straight lines ax^(2)+3xy-2y^(2)-5x+5...
Text Solution
|
- Consider a pair of perpendicular straight lines ax^(2)+3xy-2y^(2)-5x+5...
Text Solution
|