Home
Class 12
MATHS
Let f:R→R:f(x)=(x+1) and g:R→R:g(x)=(x^2...

Let `f:R→R:f(x)=(x+1)` and `g:R→R:g(x)=(x^2 −4)`. Write down the formulae for `(fog)`.

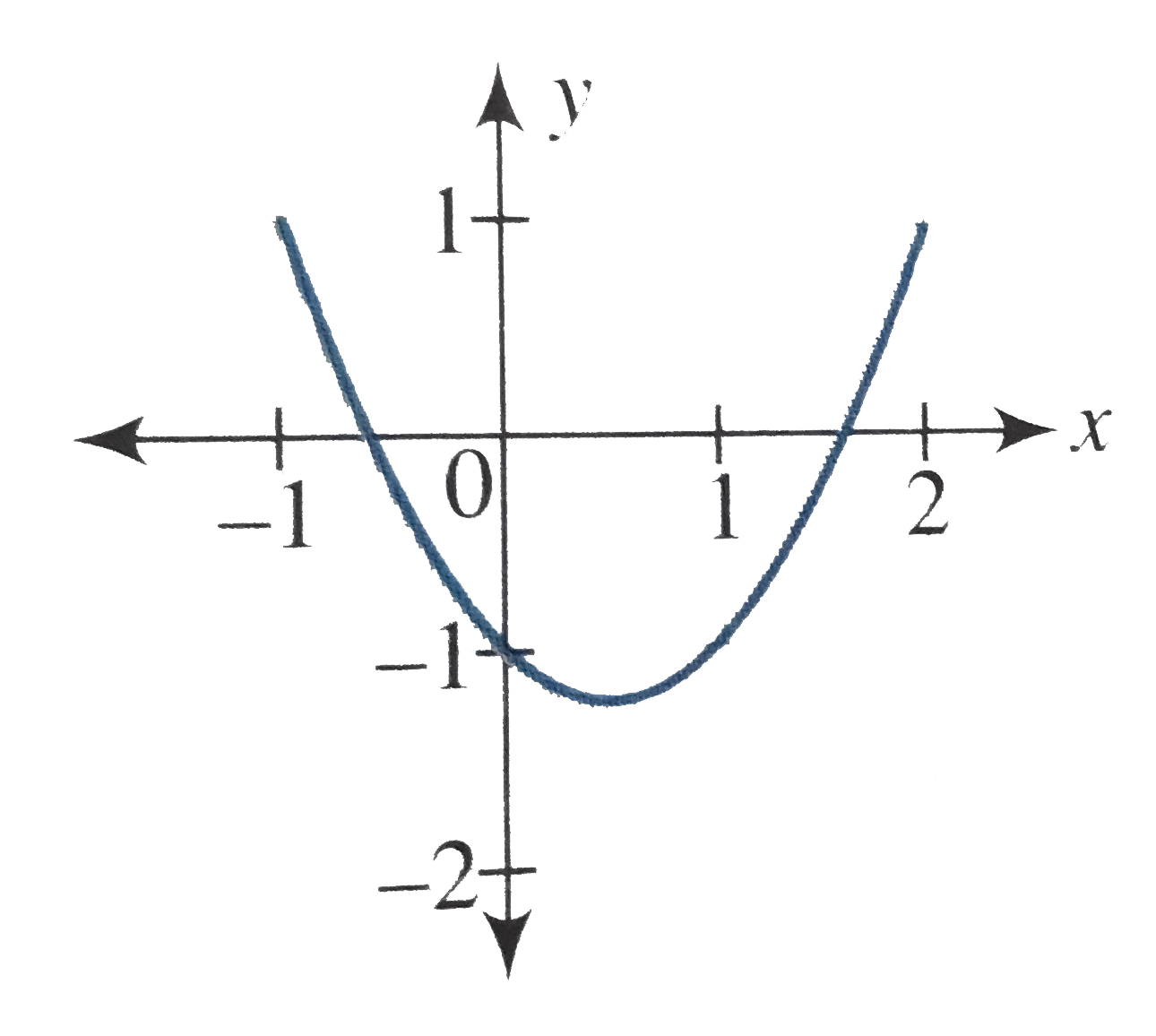
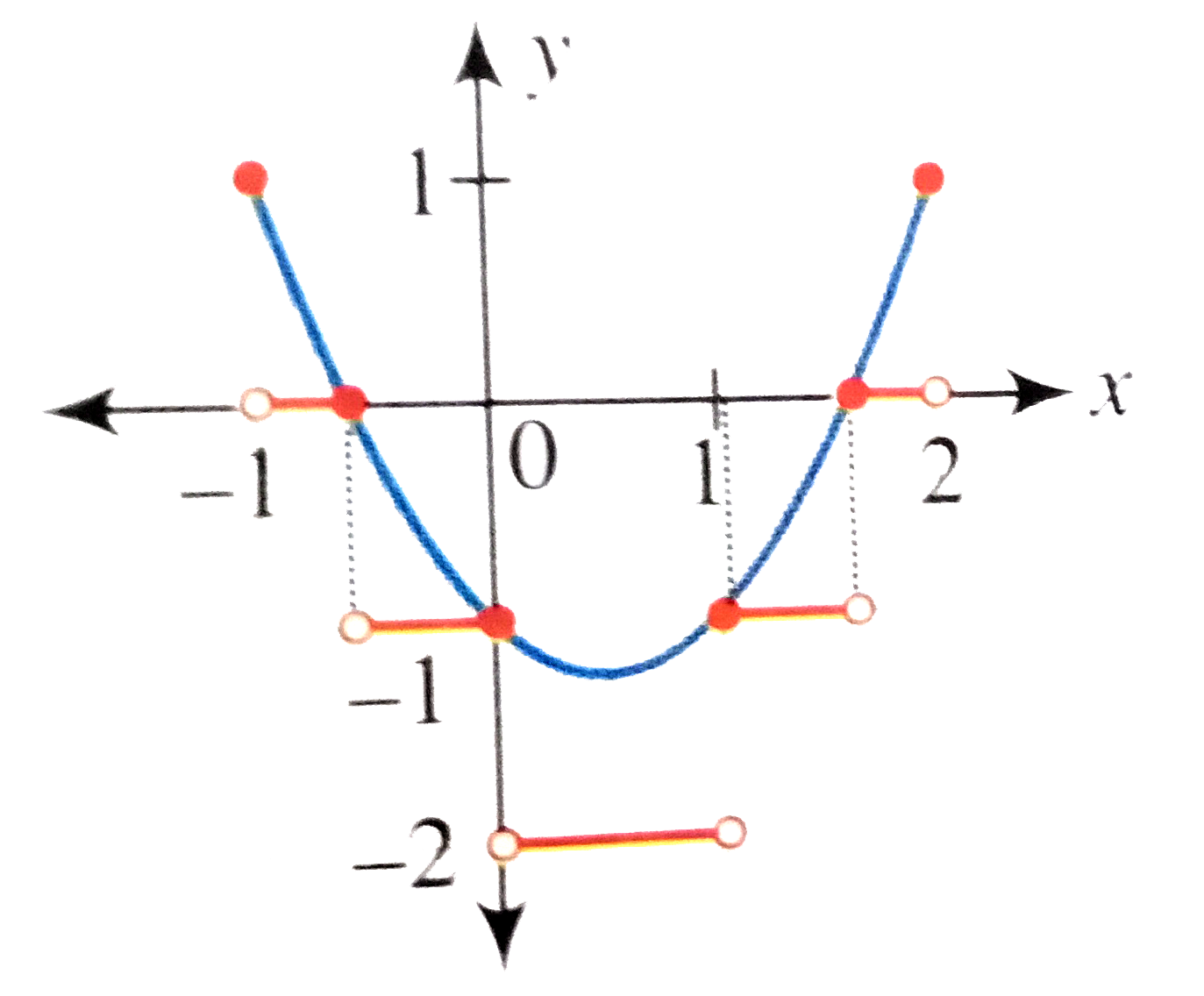
Text Solution

Verified by Experts

`f(x)=[x^(2)-x-1],x in[-1,2]`
Let us first draw the graph of `y=x^(2)-x-1`, which is an upward parabola having vertex at (1/2,-5/4).

The graph of `f(x)=[x^(2)-x-1]` can be drawn as shown in the following figure.

From the figure, `y=f(x)` is discontinuous at `x=-1,0,2 and the values of x for which `x^(2)-x-1=0orx=(1pmsqrt5)/(2)`.
Promotional Banner

Topper's Solved these Questions

  • GRAPHICAL TRANSFORMATIONS

    CENGAGE|Exercise Exercise|14 Videos

  • GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Exercise|18 Videos

  • GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS

    CENGAGE|Exercise Exercises|4 Videos

Similar Questions

Explore conceptually related problems

Let f:R→R:f(x)=(x+1) and g:R→R:g(x)=(x^2−2) . Write down the formulae for (gof) .

Let f:R→R:f(x)=x^2 and g: R→R: g(x)=(x+1) . Show that (gof)≠(fog) .

If f:R→R, g:R→R are given by f(x)=(x+1)^2 and g(x)=x^2+1 , then write the value of fog(−3) .

If A={1,2,3,4}, f:R→R=x^2+3x+1 and g:R→R,8(x)=2x−3 then find fof(x)

Let f:R rarr R, f(x)=x+log_(e)(1+x^(2)) . Then

Let f(x)=sinx and g(x)=(log)_e|x| If the ranges of the composition functions fog and gof are R_1 and R_2, respectively then (a) R_1{u:-1 le u < 1}, R_2={v:-oo v < 0} (b) R_1={u:-oo < u < 0}, R_2={v:-oo < v < 0} (c) R_1={u:-1 < u < 1},R_1={v:-oo V le 0}

If f: R to R and g: R to R are defined by f(x)=x^(5) and g(x)=x^(4) then check if f, g are one-one and fog is one-one?

If f:R^+→R^+ and g:R^+→R^+ , defined as f(x)=x^2,g(x)= sqrtx ​, then find gof and fog whether are they equivalent?

Find fog(2) and gof(1) , when f:R→R;f(x)=x^2+8 and g:R→R;g(x)=3x^3+1 .

If f :R ->R , f(x)=x^3 +3 ,and g:R->R , g(x)=2x + 1 , then f^(-1)g^(-1)(23) equals