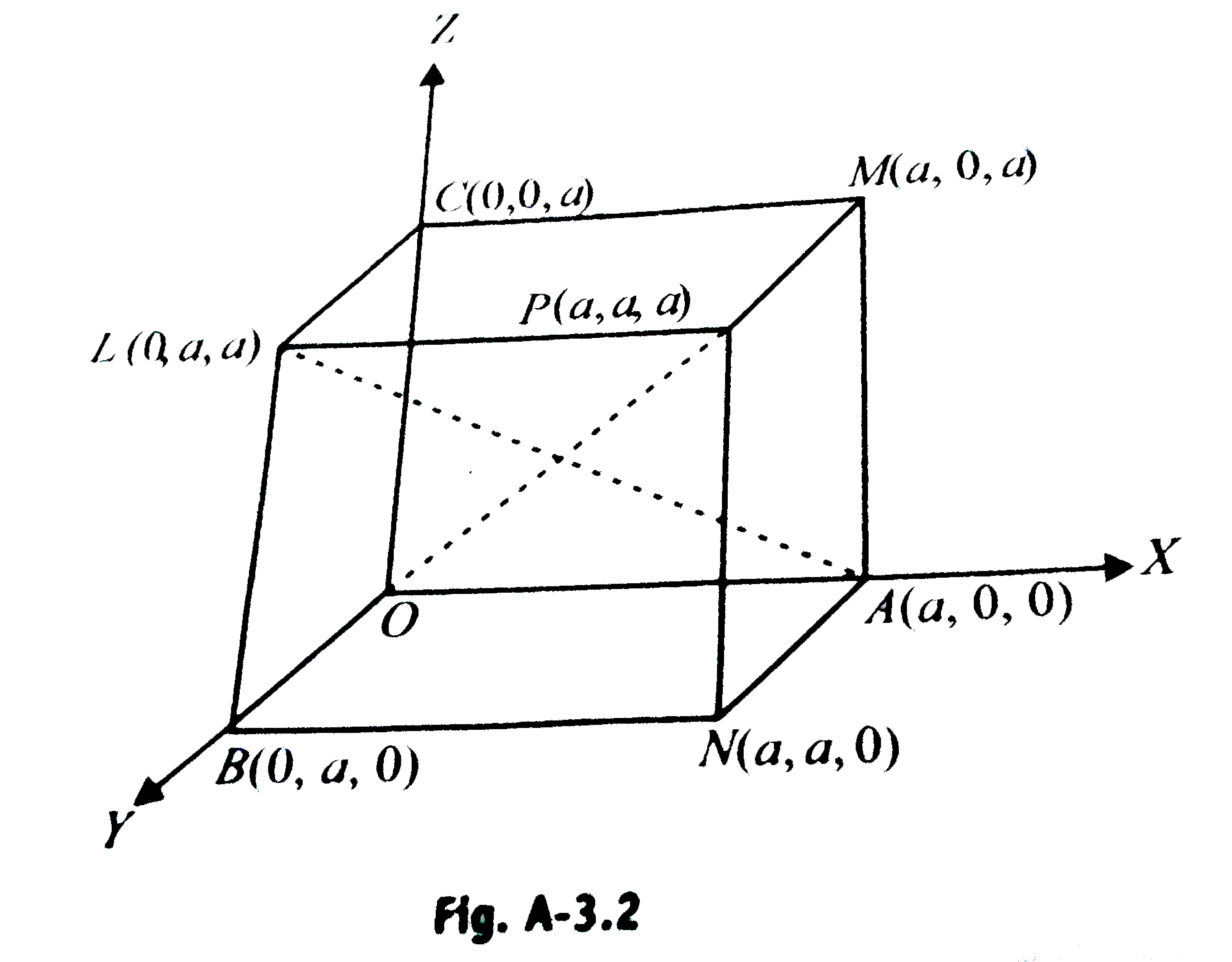Text Solution
Verified by Experts
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise 3.2|15 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise 3.3|19 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise JEE Previous Year|26 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE|Exercise Question Bank|12 VideosTRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
CENGAGE|Exercise Question Bank|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise 3.1
- If the x-coordinate of a point P on the join of Q(22,1)a n dR(5,1,-...
Text Solution
|
- Find the distance of the point P(a ,b ,c) from the x-axis.
Text Solution
|
- If vec r is a vector of magnitude 21 and has direction ratios 2,-3...
Text Solution
|
- If P(x ,y ,z) is a point on the line segment joining Q(2,2,4)a n d ...
Text Solution
|
- If O is the origin, O P=3 with direction ratios -1,2,a n d-2, then fin...
Text Solution
|
- A line makes angles alpha,beta,gamma with the coordinates axes . If al...
Text Solution
|
- The line joining the points -2,1,-8)a n d(a ,b ,c) is parallel to t...
Text Solution
|
- If a line makes angles alpha,betaa n dgamma with threew-dimensional ...
Text Solution
|
- A parallelepiped is formed by planes drawn through the points P(6,8...
Text Solution
|
- Find the angel between any two diagonals of a cube.
Text Solution
|
- Direction ratios of two lines are a ,b ,ca n d1//b c ,1//c a ,1//a ...
Text Solution
|
- Find the angle between the lines whose direction cosines are connec...
Text Solution
|