To draw the graph of `y=f(x)=(x-1)|(x-2)(x-3)|`, we first draw the graph of
`y=g(x)=(x-1)(x-2)(x-3)`
The graph of `y=g(x)` can be drawn using the sign scheme of `g(x)`.
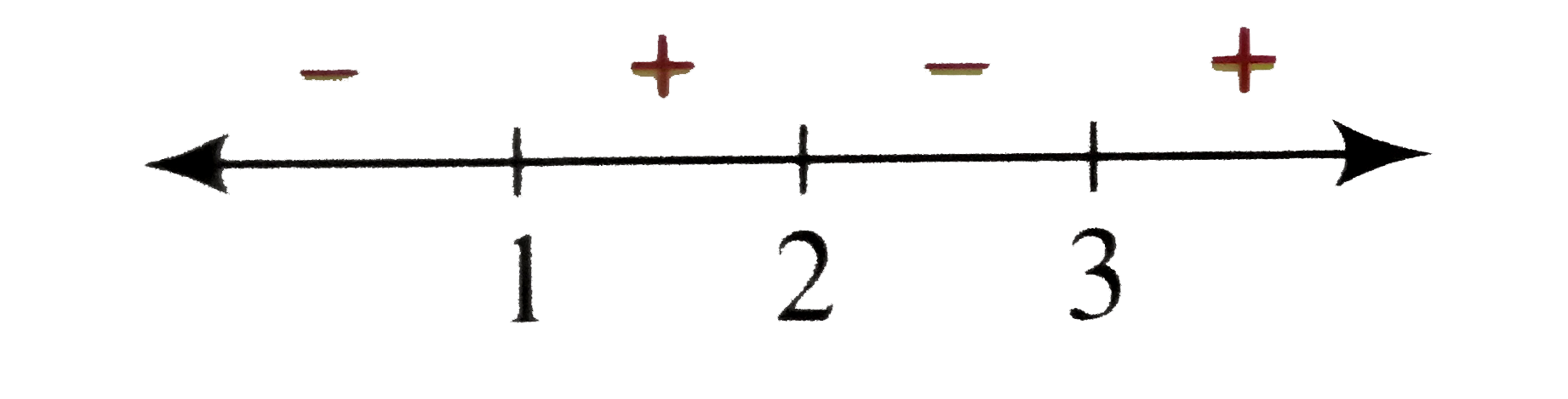
Using the sign scheme, we draw the graph of `y=g(x)` as a wave as shown in the following figure.
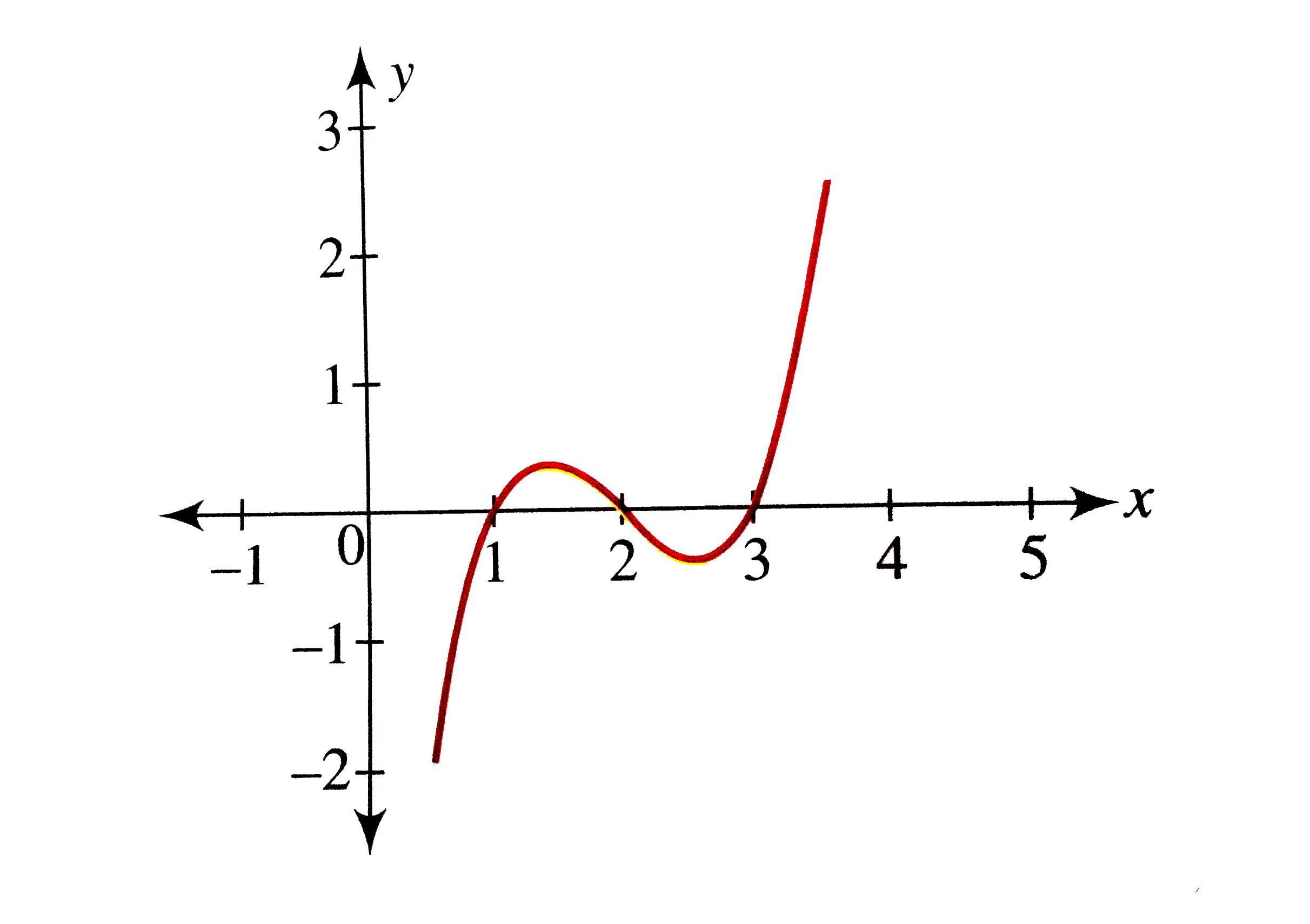
Now the sign scheme of `f(x)` is as follows.
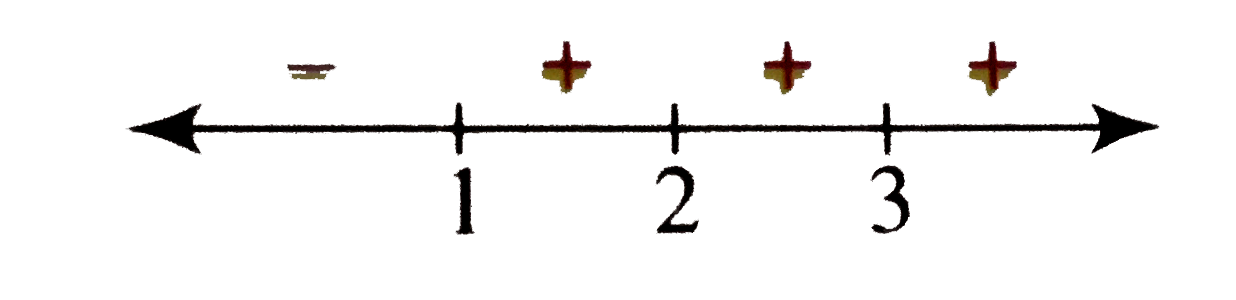
According to the above sign scheme, to draw the graph of `y=f(x)`, we reflect the graph of `y=g(x)` above the x-axis for `x in (2,3)`. So the graph of `y=f(x)` is as shown in the following figure.
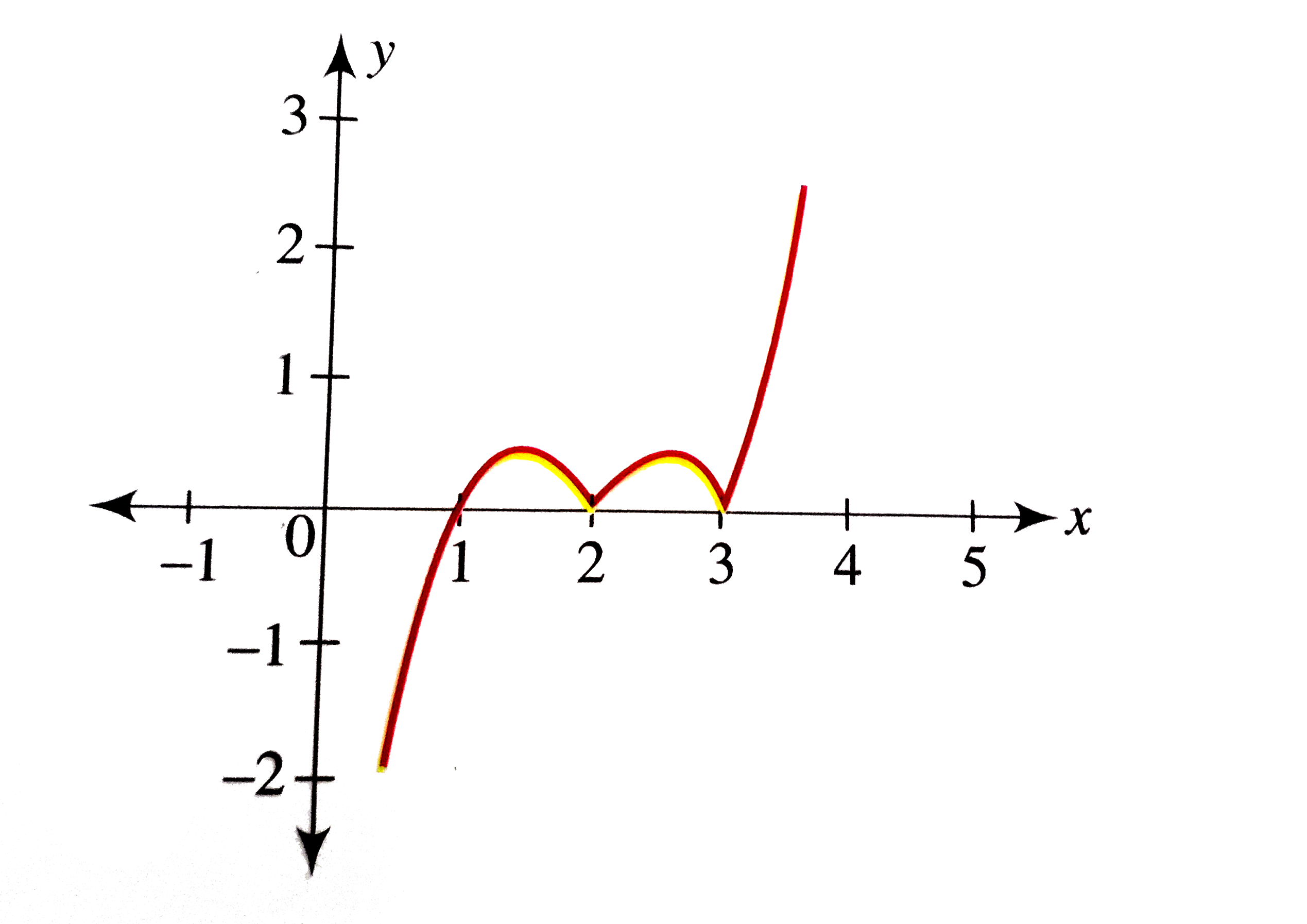
For `g(x)=(x-1)(x-2)(x-3)`
`=x^(3)-6x^(2)+11x-6`
`g'(x)=3x^(2)-12x+11`
`g'(x)=0 :. x=(12+-sqrt(144-132))/(6)=(12+-sqrt(12))/(6)=2+-(1)/(sqrt(3))`
Thus, `x=2-(1)/(sqrt(3))` and `x=2+(1)/(sqrt(3))`, points of local maxima and local minima, respectively, for `y=g(x)`.
For `y=f(x),x=2+-(1)/(sqrt(3))` are the points of local maxima.