To examine the roots of the equation `x^(4)-14x^(2)+24x-3-p=0` , let us first draw the graph of the function.
`f(x)=x^(4)-14x^(2)+24x-3`
`f'(x)=4x^(3)-28x+24`
`=4(x^(3)-7x+6)`
`=4(x^(3)-x^(2)+x^(2)-x-6x+6)`
`=4(x-1)(x^(2)+x-6)`
`=4(x-1)(x+3)(x-2)`
`f'(x)=0 :. x=1, 2, -3`
Also the leading coefficient is 1, when `x rarr +- oo , f(x) rarr oo`.
Sign scheme of `f'(x)` is as follows.
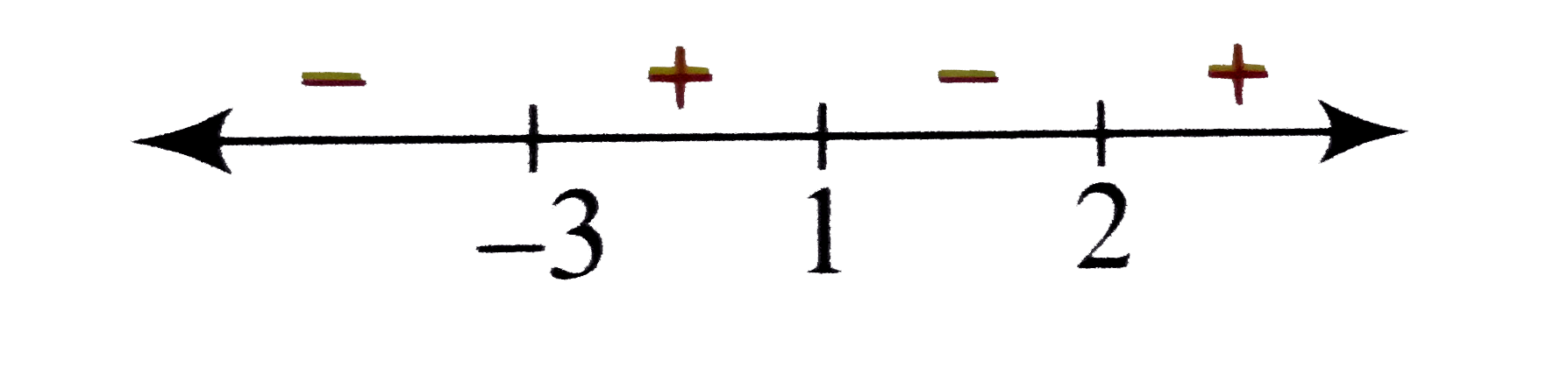
Clearly, from the sign scheme, x = -3 and x = 2 are the points of minima and x = 1 is the point of maxima.
`f(1)=8,f(2)=5` and `f(-3)=-120`
Also `f(0)=-3`
So the graph of `y=f(x)` is as shown in the following figure.

Now to examine the roots of the equation `x^(4)-14x^(2)+24x-3=p`, we draw the straight line y = p and find the intersection of `y=f(x)` and `y=p`.
Now for two distinct negative real roots of `f(x)=p, y=p` must cu t`y=f(x)` between point C and the x-axis. Hence the values of 'p' for two negative roots are (-120,0).
For two real roots of opposite sign, y = p must cut y = f(x) between points H and D. Hence the values of 'p' for two real roots of opposite sign are (-3,5).
For four distinct real roots, y=p must cut `y=f(x)` four times between points H and F. Hence the values of 'p' are (5,8).
For no real roots, `y=p` must lie below point C. Hence the values of 'p' are `(-oo,-120)`.

