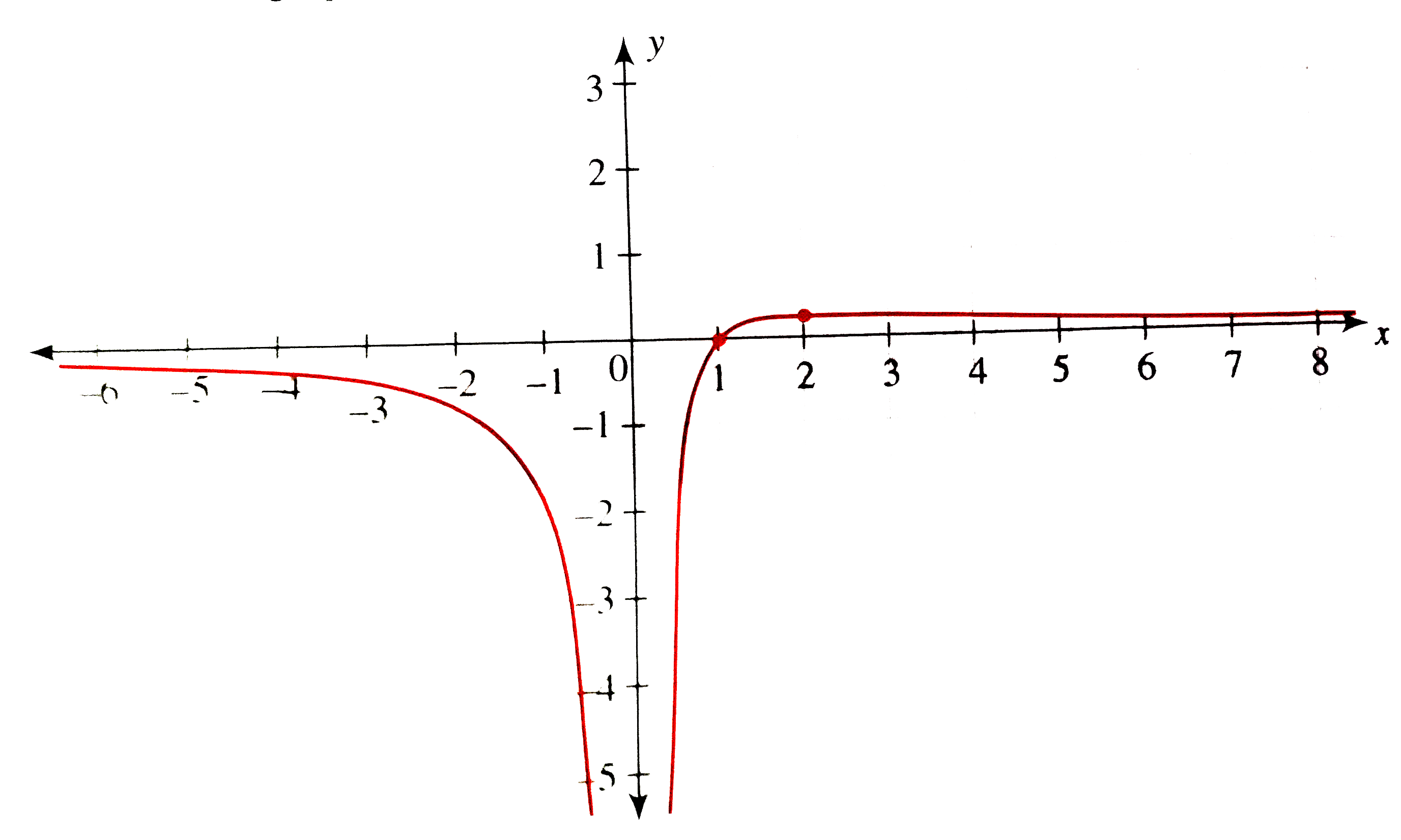
The domain of function is R - {0}.
1. y-intercept
Graph never intersects the y-axis as the domain does not contain x = 0.
2. x-intercept (zeros)
Put y = 0 or x - 1 =0
Hence the graph intersects the x-axis at (1, 0).
3. Asymptotes
Vertical asymptotes
Graph has vertical asymptote x = 0.
Horizontal asymptotes
Since the degree of the denominator is higher than the degree of the denominator , the graph has horizontal asymptote y = 0.
Clearly , the graph has no oblique asymptote.
4. Extremum
`f'(x)=(2x-x^(2))/(x^(4))=(2-x)/(x^(3))`
`f'(x)=0rArr x=2`
Sign scheme of `f'(x)` is as follows.
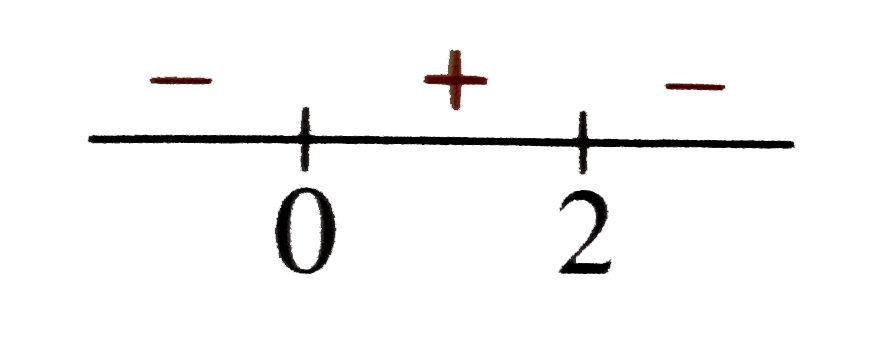
From the sign scheme, x = 2 is the point of maxima.
Also `f(2)=(1)/(4)`
From the above discussion, we have the following reference points and lines.

When `x rarr -oo, y rarr 0` and when `xrarr0^(-), y rarr -oo`. So `f(x)` decreases from '0' to `'-oo'` in `(-oo,0)`.
When `x rarr 0^(+), y rarr -oo`, so `f(x)` increases from `'-oo'` ot '1/4', intersecting the x-axis at (1, 0).
`f(x)` attains the maximum value at x = 2 and then decreases to approach '0' as x approaches `'oo'` as `underset(xrarroo)lim (x-1)/(x^(2))=0`.
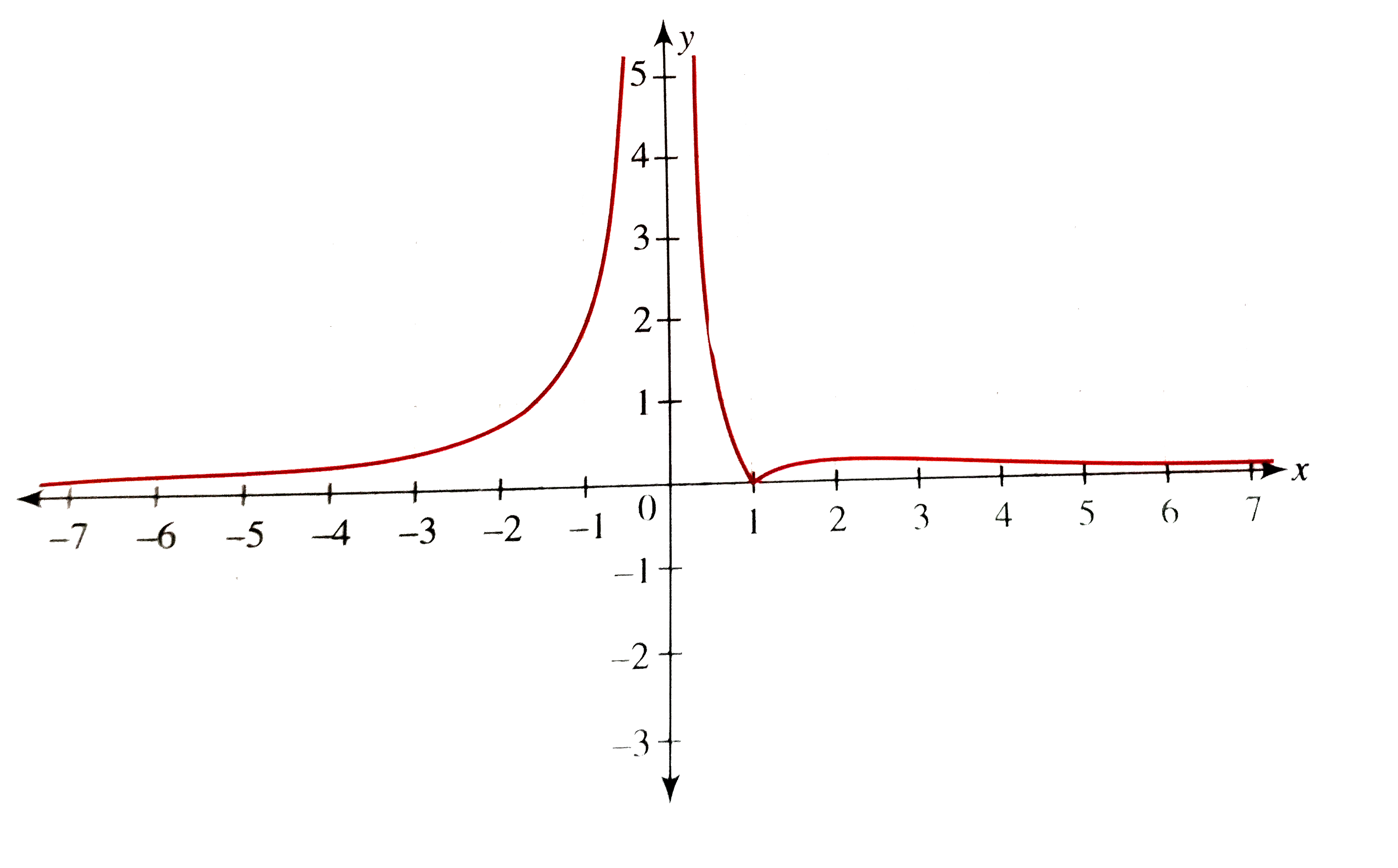
Thus , the graph of `y=f(x)` is as shown in the following figure.
To draw the graph of `y=g(x)=(|x-1|)/(x^(2))=|f(x)|`, flip the portion of the graph which is below the x-axis over the x-axis.
So the graph of y = g(x) is as follows .