`f(x)=(1)/(x^(2)-2x+2)`
`=(1)/((x-1)^(2)+1) gt 0, AA x in R`
`f(0)=1`, hence the graph intersects the y-axis at (0,1).
`f(x)!=0` for any real x, hence the graph never intersects the x-axis.
Further `x^(2)-2x+2!=0` for any real x, hence the function has no verical asymptote.
Also the degree of the denominator is higher than the degree of the numerator, hence the graph has horizontal tangent x = 0.
`f'(x)=(2x-2)/((x^(2)-2x+2)^(2))`
`f'(x)=0 :. x=1`, which is the point of maxima.
For `x in (-oo,1),f(x)` increases and for `x in (1, oo), f(x)` decreases.
Also `f(1)=1`
From the above discussion, the graph of the function is shown in the following figure.
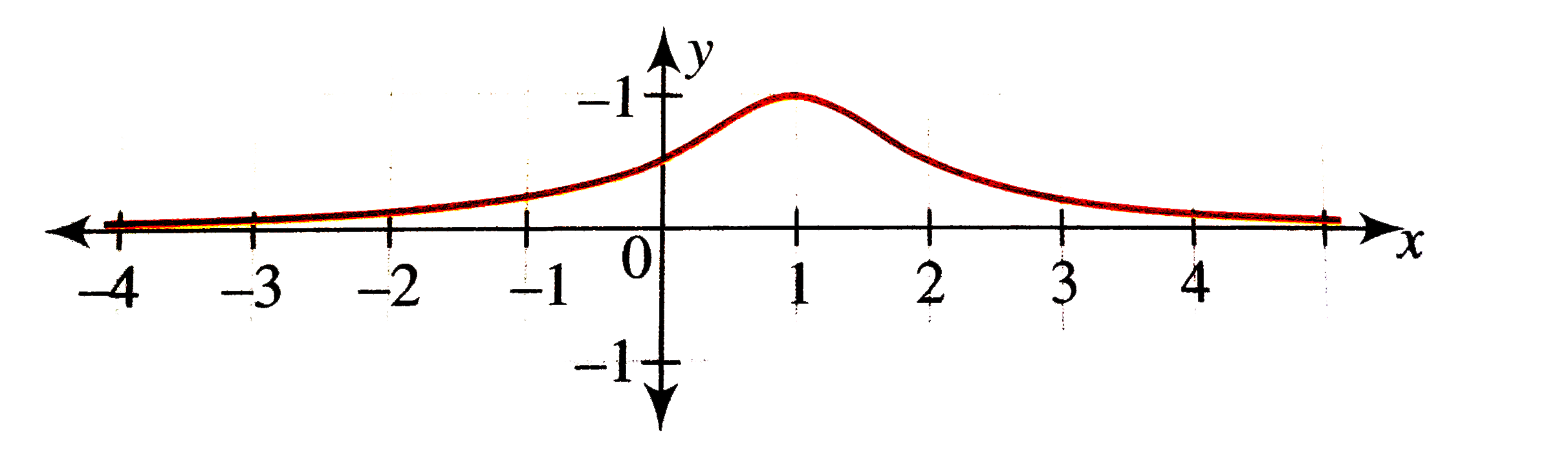
Since `f(1-x)=f(1+x)`, the graph is symmetrical about the line x = 1.