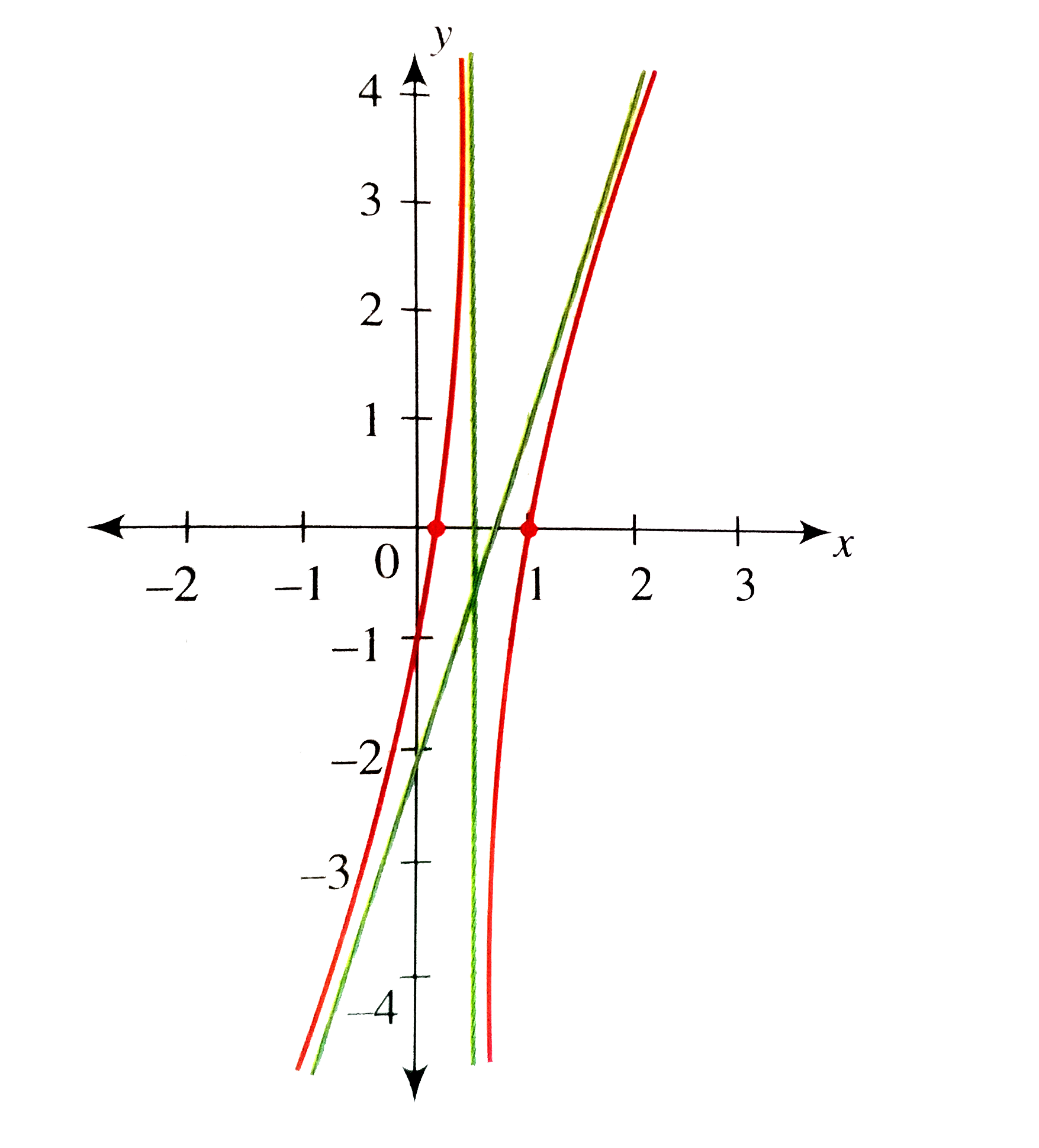
We have `y=f(x)=((x-1)(6x-1))/(2x-1)`.
The domain of the function is `R-{1//2}`.
1. y-intercept `f(0)=1` So the graph cuts the y-axis at (0,-1).
2. x-intercept (zeros)
Put `y=0` or ` (x-1)(6x-1)=0`
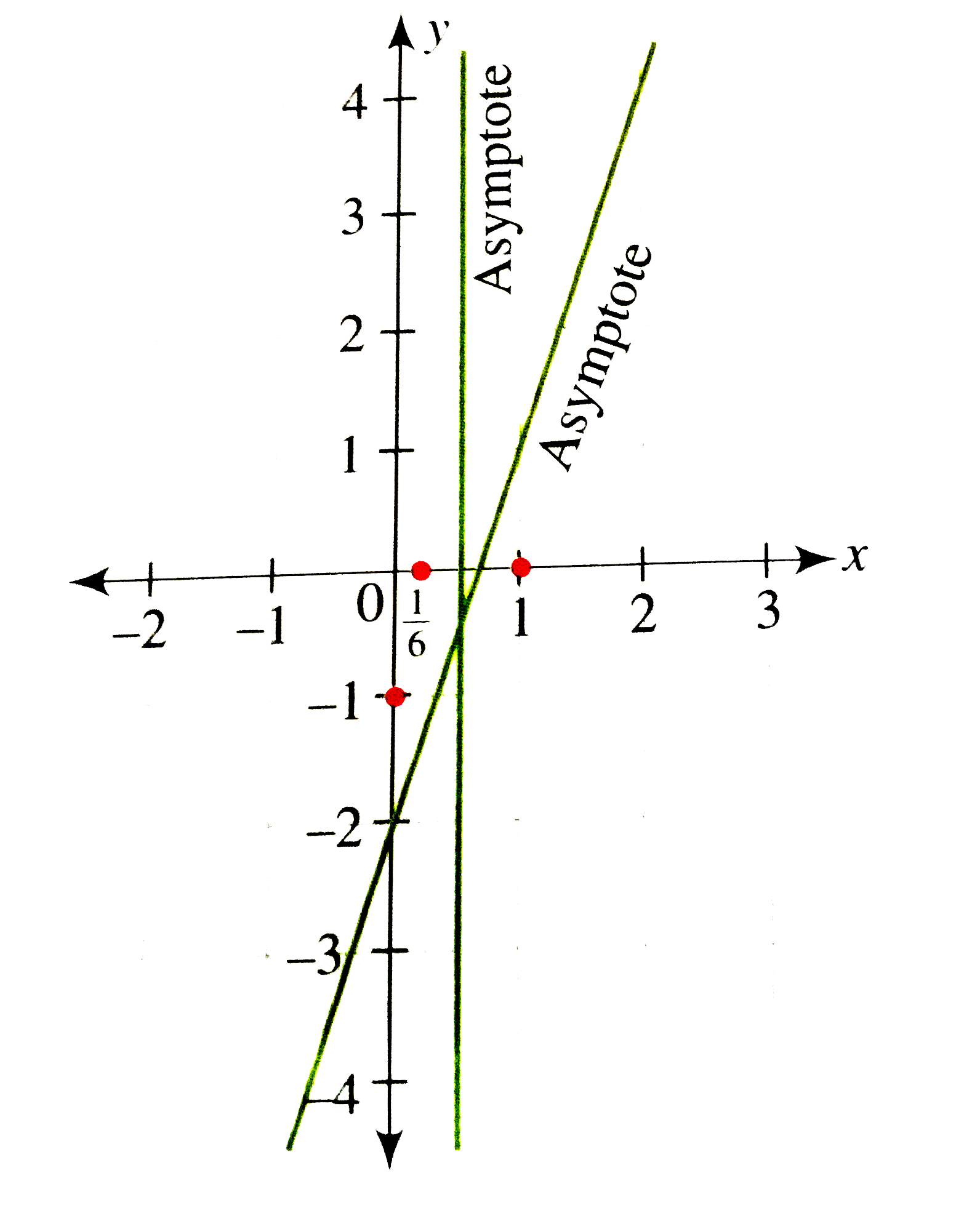
So the graph meets the x-axis at (1/6,0) and (1,0).
3. Asymptotes
Vertical asymptotes
Clearly, the graph has vertical asymptote x = 1/2, where the denominator becomes zero.
Horizontal asymptotes Clearly, the graph has no horizontal asymptote.
Oblique asymptotes
`y=(6x^(2)-7x+1)/(2x-1)`
`=3x-2-(1)/(2x-1)`
Thus, important points and lines are as follows.
4. Momotonicity/Extremum
`f'(x)=((12x-7)(2x-1)-2(6x^(2)-7x+1))/((2x-1)^(2))`
`=((12x^(2)-12x+5))/((2x-1)^(2)) gt0, AA x in R-{1//2}`
Hence the function is increasing throughout.
`underset(xrarr-oo)lim((x-1)(6x-1))/(2x-1)=-oo` and `underset(xrarr(1^(-))/(2))lim ((x-1)(6x-1))/(2x-1)=oo`
Thus, f(x) increases from `-oo` to `oo` when x increases from `-oo` to 1/2 crossing the x-axis at (1/6,0) and approaching asymptote `y=3x-2` to the left of it.
`underset(xrarr(1^(+))/(2))lim ((x-1)(6x-1))/(2x-1)=-oo` and `underset(xrarroo)lim ((x-1)(6x-1))/(2x-1)=oo`
Thus, f(x) increases from `-oo` to `oo` when x increases from 1/2 to `oo` crossing the x-axis at (1,0) . f(x) approaches asymptote `y=3x-2` to the right of the asymptote.
Hence the graph of `y=f(x)` can be drawn as shown in the following figure.