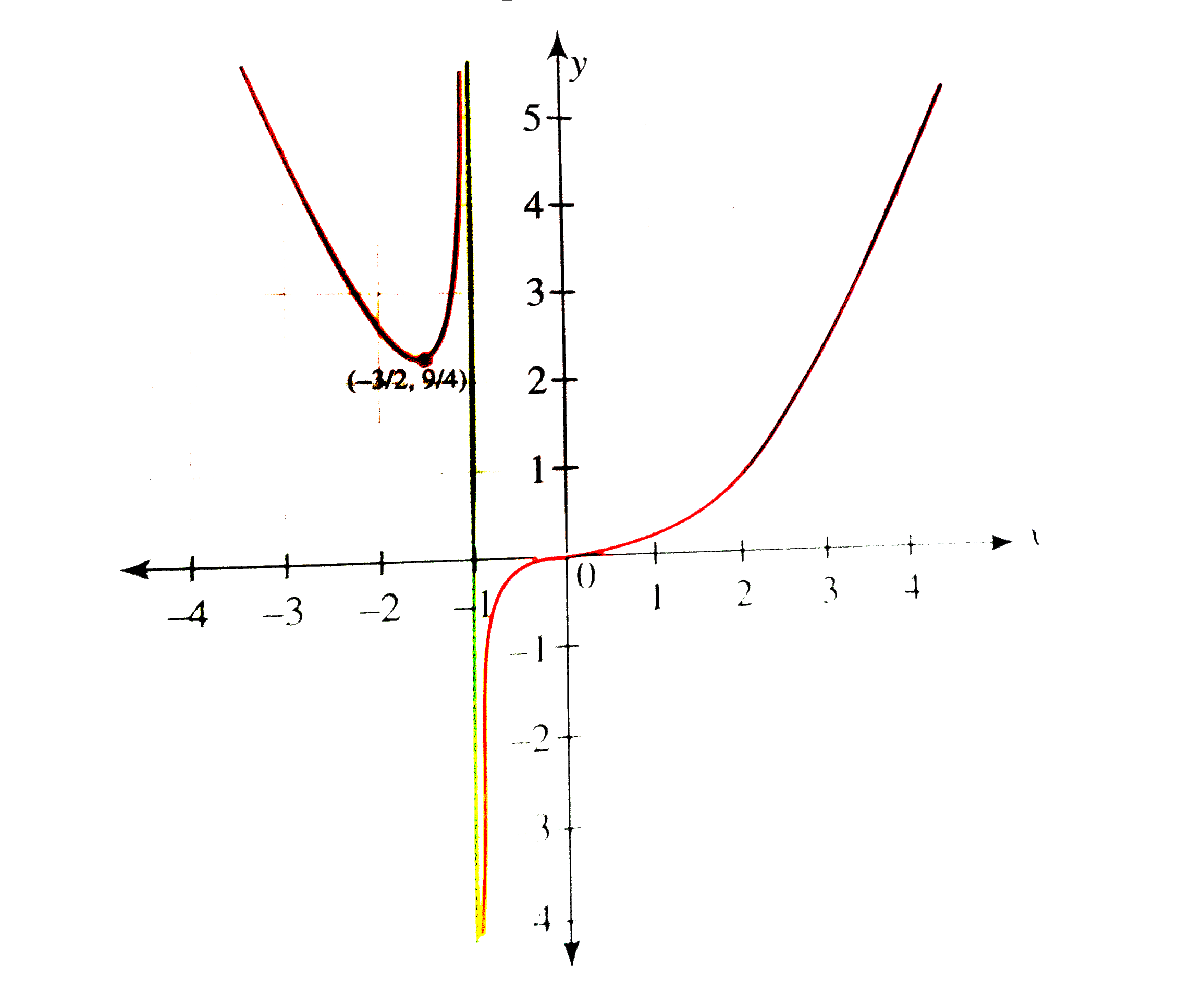
We have `y=f(x)=(x^(3))/(3(x+1))`
Domain of the function is R-{-1}.
Graph cuts the axis at (0,0).
It has vertical asymptote x=-1, where the denominator becomes Zero.
Cleary, the graph has no horizontal and oblique asymptote.
`f'(x)=(3x^(2)(x+1)-x^(3))/(3(x+1)^(2))=(x^(2)(2x+3))/(3(x+1)^(2))`
`f'(x)=0 :. x=0,-3//2`
`f'(x) gt 0` for `x gt -3//2`. So the function increases in `(-3//2,oo)-{-1}`.
`f'(x) lt 0` for `x lt -3//2`. So the function decreases in `(-oo,-3//2)`.
`x=-3//2` is the point of minima.
`f'(0)=0` but x=0 is not a point of minima/maxima, so it is the point of inflection where the curve changes its concavity.
`underset(xrarr-oo)lim(x^(3))/(x+1)=oo, f(-3//2)=9//4`
Thus, f(x) decreases from `'oo'` to '9/4' in `(-oo,-3//2)`.
`underset(xrarr-1^(-))lim(x^(3))/(x+1)=oo`
Thus, `f(x)` increases from '9/4' to `'oo'` in (-3/2,-1).
`underset(xrarr-1^(-))lim (x^(3))/(x+1)=-oo` and `underset(xrarroo)lim(x^(3))/(x+1)=oo`
Thus, `f(x)` increases from `'-oo'` to `'oo'` in `(-1,oo)` intersecting the x-axis at (0,0) and having point inflection as well at this point.
From the above discussion, the graph of `y=f(x)` can be drawn as follows.