Given line is 3x-4y-a(a-2)=0
One of the possible lines is as shown in the following figure.
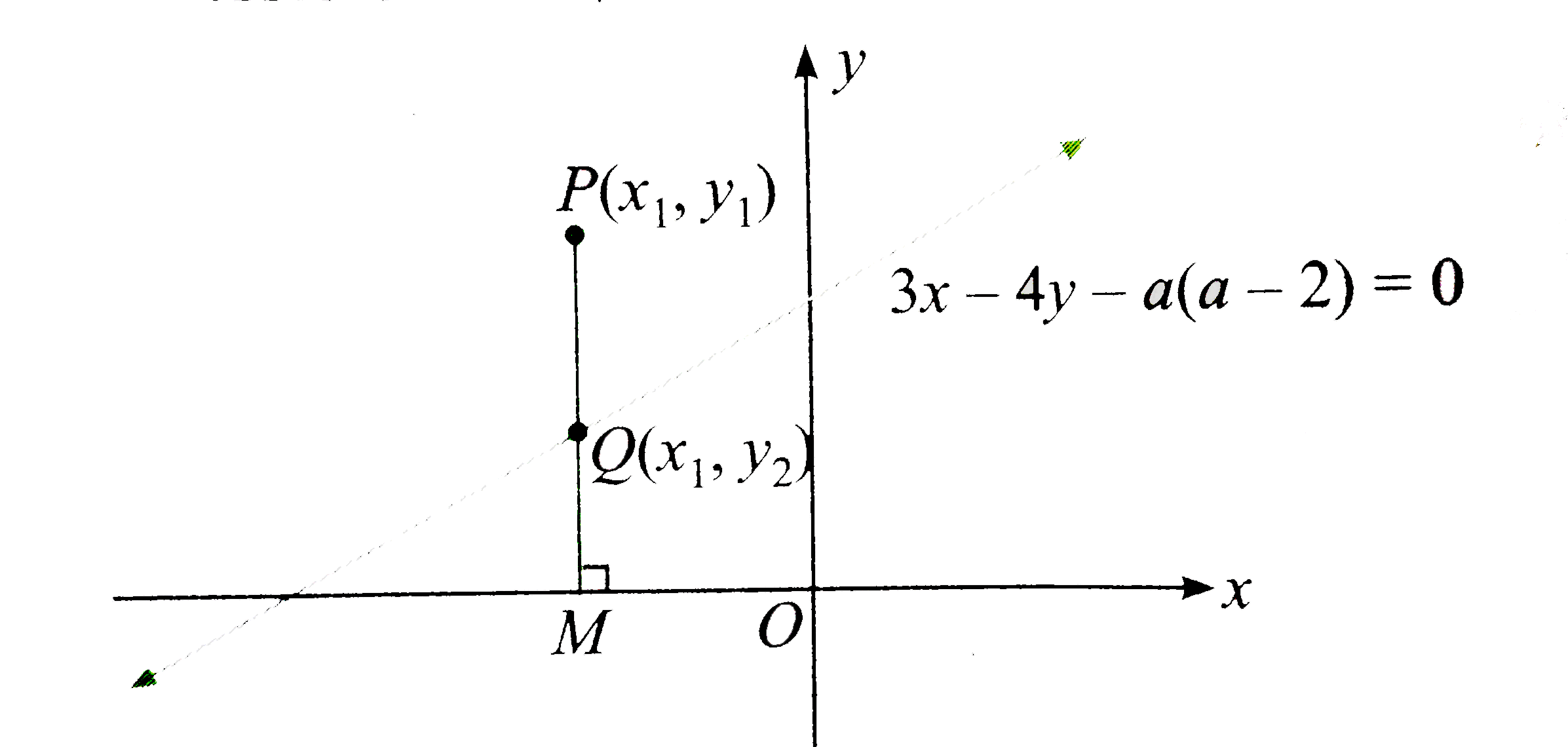
Consider the point `P(x_(1), y_(1))` lying above this line.
Draw perpendicular from point P to the x-axis meeting the line at `Q(x_(1), y_(2))" and x-axis at M"`
`"Clearly, PM" gt QM`
`therefore y_(1) gt y_(2)`
`rArr -4y_(1) lt -4y_(2)`
`rArr 3x_(1)-a(a-2)-4y_(1) lt 3x_(1) -a(a-2)-4y_(2)`
`rArr 3x_(1)-a(a-2)-4y_(1) lt 0 " " ("As point Q lies on the line")`
`rArr 3(2b+3)-a(a-2)-4b^(2) lt 0, AAa in R`
`" " ("Putting " x_(1) = 2b +3 " and "y_(1) = b^(2))`
`a^(2)-2a+4b^(2)-6b-9 gt 0 AA a in R`
`therefore " Discriminant" lt 0`
`rArr 4-4(4b^(2)-6b-9) lt 0`
`rArr 1-4b^(2) + 6b+9) lt 0`
`rArr 2b^(2)-3b-5 gt 0`
`rArr (2b-5)(b+1) gt 0`
`rArr b in (-oo, -1) uu ((5)/(2), oo)`