Home
Class 12
MATHS
In triangleABC, vertex A is (1, 2). If t...

In `triangleABC`, vertex A is (1, 2). If the internal angle bisector of `angle B` is `2x- y+10=0` and the perpendicular bisector of AC is y = x, then find the equation of BC

Text Solution

Verified by Experts

The image D of A in the bisector of `angle B` lies on BC.
Now, the image of A(1,2) in the line 2x-y-10=0 is given by
`(x_(1)-1)/(2) = (y_(1)-2)/(-1) = (-2(2-2+10))/(4+1)`
. `therefore D(x_(1), y_(1)) -=D(-7,6)`

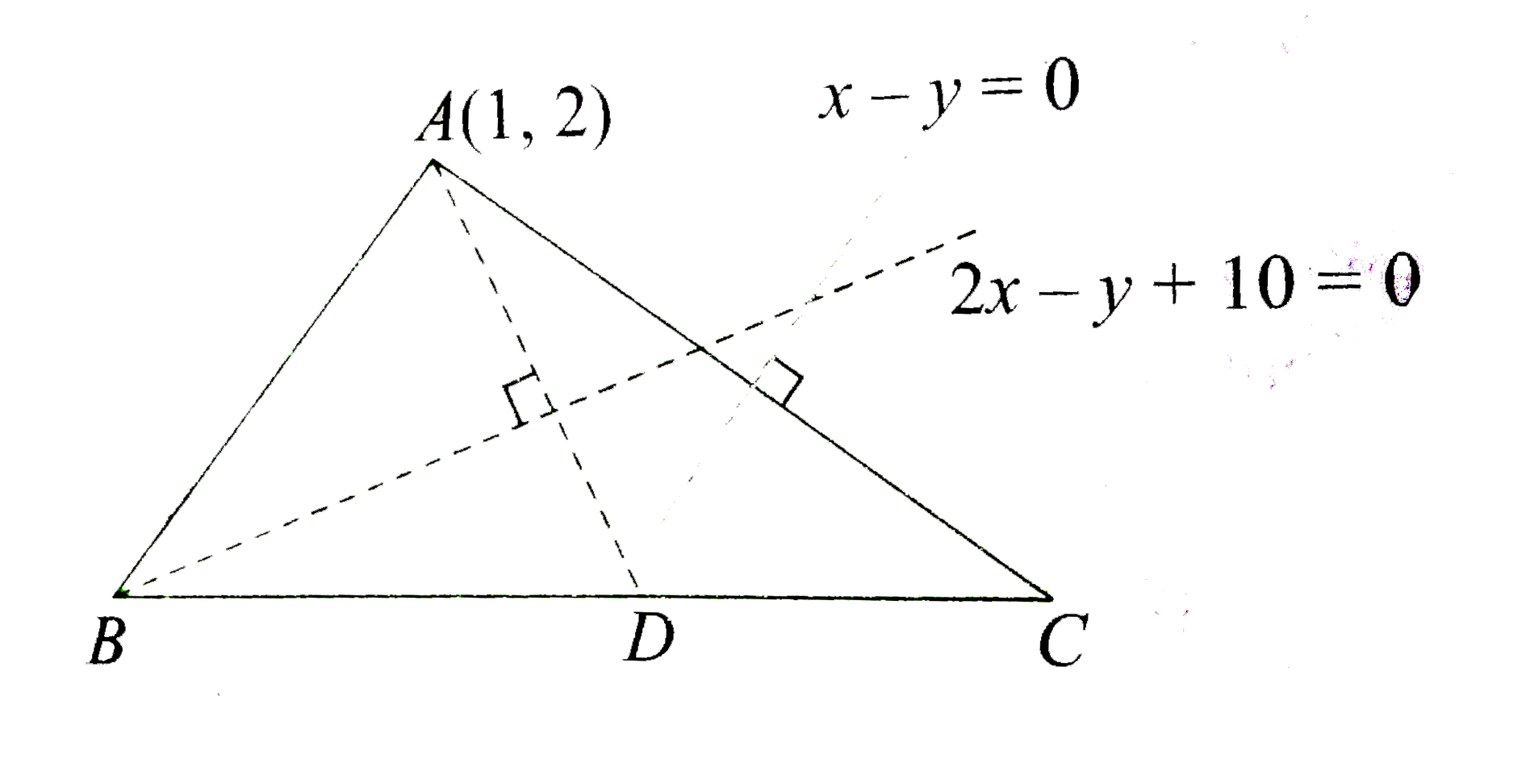
Also, C is the image of A in the perpendicular bisector of AC. The image of A(1,2) in y=x is C(2,1).
Hence the equation of line BC is
. `y-1 = (6-1)/(-7-2)(x-2)`
or 5x+9y-19=0
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.1|23 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.2|4 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

Line x + 2y - 8 = 0 is the perpendicular bisector of AB. If B = (3, 5) the A is

Let A B C be a triangle. Let A be the point (1,2),y=x be the perpendicular bisector of A B , and x-2y+1=0 be the angle bisector of /_C . If the equation of B C is given by a x+b y-5=0 , then the value of a+b is (a) 1 (b) 2 (c) 3 (d) 4

In triangle A B C , the equation of the right bisectors of the sides A B and A C are x+y=0 and y-x=0 , respectively. If A-=(5,7) , then find the equation of side B Cdot

In triangle ABC, the coordinates of the vertex A are , (4,-1) and lines x - y - 1 = 0 and 2x - y = 3 are the internal bisectors of angles B and C . Then the radius of the circles of triangle AbC is

Let A,B,C be angles of triangles with vertex A -= (4,-1) and internal angular bisectors of angles B and C be x - 1 = 0 and x - y - 1 = 0 respectively. If A,B,C are angles of triangle at vertices A,B,C respectively then cot ((B)/(2))cot .((C)/(2)) =

In a triangle ABC, D is a point on BC such that AD is the internal bisector of angle A . Let angle B = 2 angle C and CD = AB. Then angle A is

The vertex A of DeltaABC is (3,-1). The equation of median BE and angle bisector CF are x-4y+10=0 and 6x+10y-59=0, respectively. Equation of AC is

The equations of the perpendicular bisectors of the sides A Ba n dA C of triangle A B C are x-y+5=0 and x+2y=0 , respectively. If the point A is (1,-2) , then find the equation of the line B Cdot

A line L passing through the point (2, 1) intersects the curve 4x^2+y^2-x+4y-2=0 at the point Aa n dB . If the lines joining the origin and the points A ,B are such that the coordinate axes are the bisectors between them, then find the equation of line Ldot