Two sides of a rhombus lying in the first quadrant are given by `3x-4y=0a n d12 x-5y=0` . If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.

Explanation

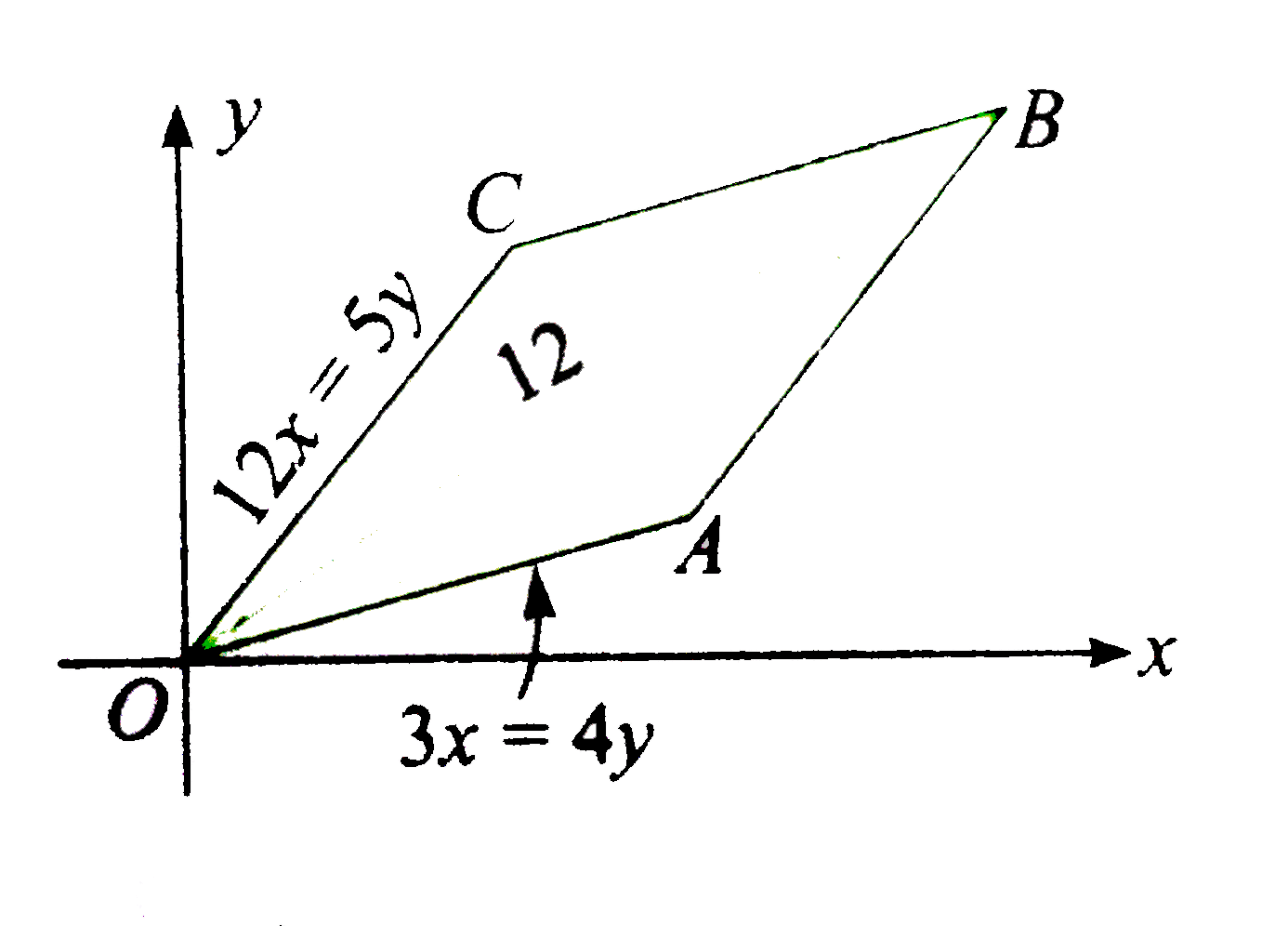
OB is along the acute angle bisector of the given lines: 3x-4y=0 and 12x-5y =0.
The equation of acute angle bisector is
`(3x-4y)/(5) = -(12-5y)/(13)`
or 9x-7y=0
`therefore "Slope of OB" = tan theta = (9)/(7)`
Now, OB= 12.
Therefore, the coordinates of B are
`(12 "cos" theta, 12 "sin" theta) -= (12(7)/(sqrt(130)), 12(9)/(sqrt(130))) -= ((84)/(sqrt(130)), (108)/(sqrt(130)))`
AB is passing through B and is parallel to OC.
Therefore, the equation of AB is
`y-(108)/(sqrt(130)) = (12)/(5)(x-(84)/(sqrt(130)))`
BC is passing through B and is parallel to OA.
Therefore, the equation of BC is `y-(108)/(sqrt(130)) = (3)/(4)(x-(84)/(sqrt(130)))`