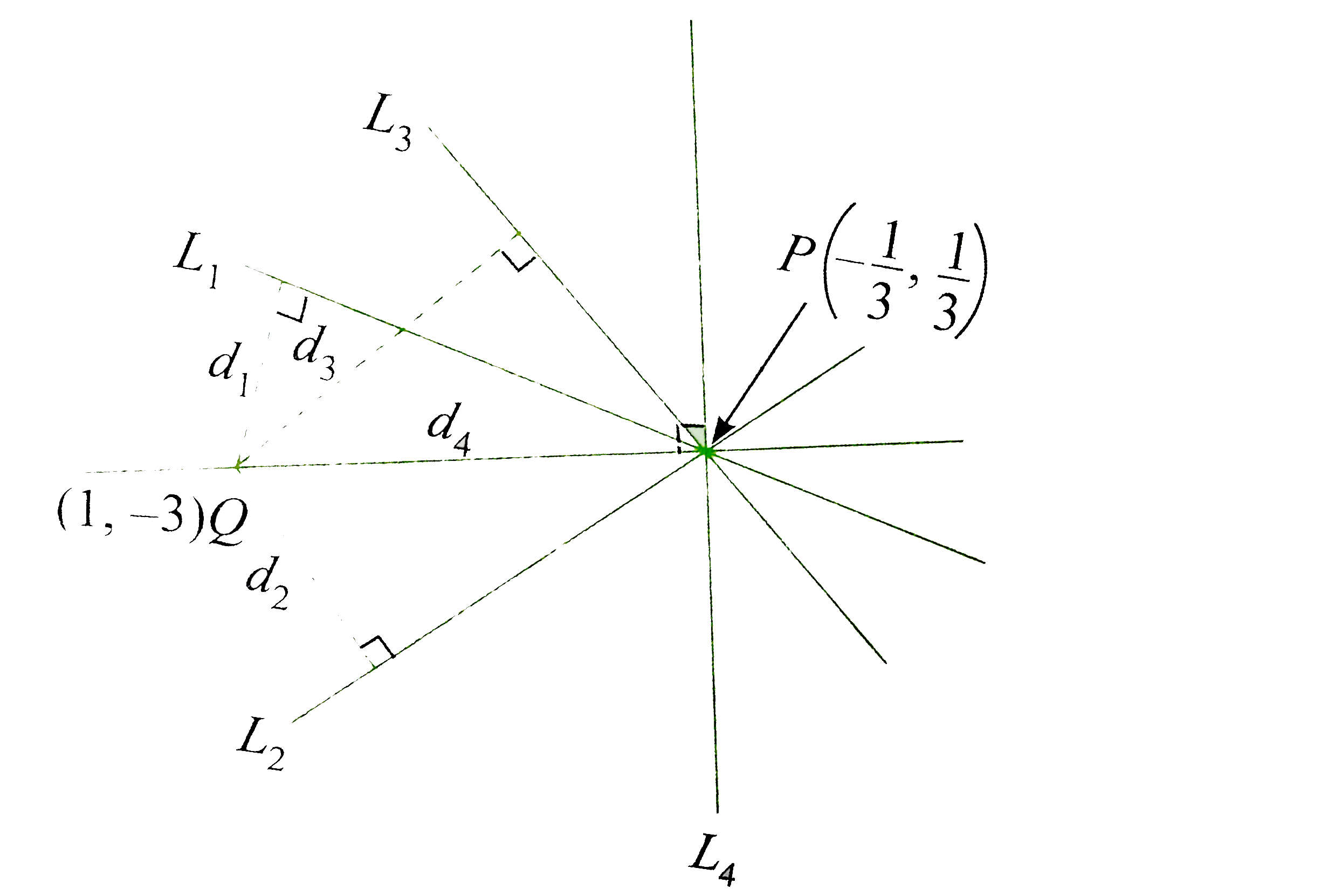
Given lines are concurrent at point of intersection of lines `x+y=0 and 2x-y+1=0 " which is P" (-(1)/(3),(1)/(3))`.
We require a line through point P which is farthest from point Q(1,-3), i.e., line whose perpendicular distance from point P is the greatest.
We observe that perpendicular distances `d_(1), d_(2),d_(3)`..... of the lines `L_(1), L_(2),L_(3)`....., respectively, from point Q are less than distance `d_(4)` of the line `L_(4)` Q. Line `L_(4)` is perpendicular to the segment joining P and Q. Line `L_(4)` is the greatest distance from point Q.
`"Slope of PQ is " m_(PQ) = (-3-(1)/(3))/(1+(1)/(3)) = -(5)/(2)`
`"Slope of the line " L_(4) = (2)/(5)`
Therefore, equation of the required line is
`y-(1)/(3)=(2)/(5)(x+(1)/(3))`
or 6x-15y+7 = 0