Home
Class 12
MATHS
Let A B C be a triangle with A B=A Cdot ...

Let `A B C` be a triangle with `A B=A Cdot` If `D` is the midpoint of `B C ,E` is the foot of the perpendicular drawn from `D` to `A C ,a n dF` is the midpoint of `D E ,` then prove that `A F` is perpendicular to `B Edot`

Text Solution

Verified by Experts


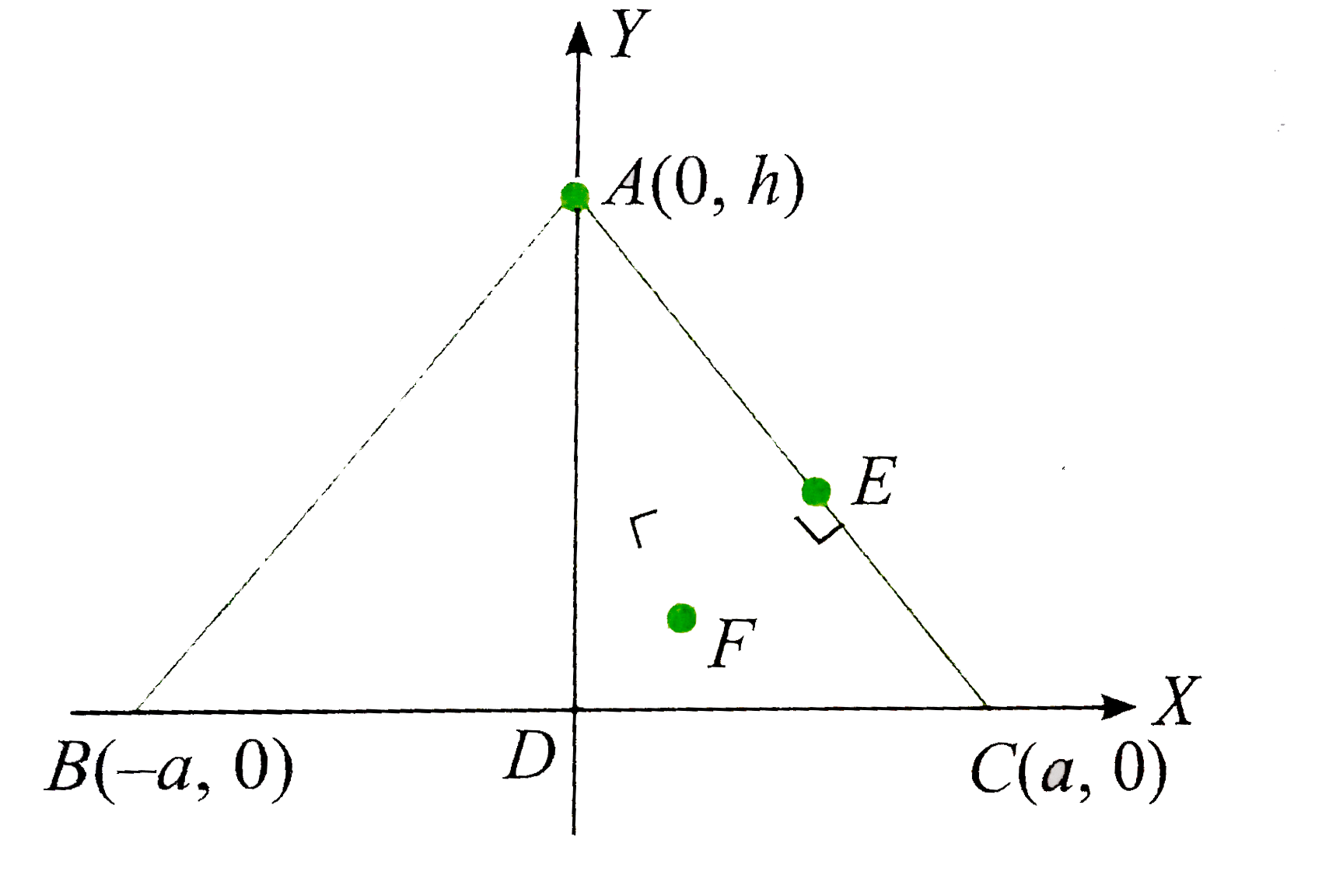
Let BC be taken as the x-axis with the origin at D. Let A be taken on y-axis. Let BC=2a. Now AB=AC, then the coordinates of B and C are (-a,0) and (a,0), respectively. Let DA =h. Then the coordiantes of A are (0,h).
Hene, the equation of AC is ltbgt `(x)/(a)+(y)/(h)=1 " " (1)`
and the equation of DE perpendicular to AC and passing through the origin is
`(x)/(h)-(y)/(a)=0`
`" or " x=(hy)/(a) " " (2)`
Solving (1) and (2), we get the coordinates of E as follows:
`(hy)/(a^(2)) +(y)/(h)=1`
`" or " h^(2)y+a^(2)y = a^(2)h`
`" or " y=(a^(2)h)/(a^(2) + h^(2)) `
`therefore x=(ah)/(a^(2) + h^(2)) `
`therefore E-=((ah^(2))/(a^(2) + h^(2)),(a^(2)h)/(a^(2) + h^(2))) `
Since F is the midpoint of DE, its coordinates are
`((ah^(2))/(2(a^(2) + h^(2))),(a^(2)h)/(2(a^(2) + h^(2)))) `
The slope of AF is
`m_(1) = (h-(a^(2)h)/(2(a^(2)+h^(2))))/(0-(ah^(2))/(2(a^(2)+h^(2))))`
`(2h(a^(2) +h^(2))-a^(2)h)/(-ah^(2)) = (a^(2) + 2h^(2))/(ah) " " (1)`
and the slope of BE is
`m_(2) = ((a^(2)h)/(a^(2)+h^(2))-0)/((ah^(2))/(a^(2)+h^(2)) + a)`
`= (a^(2)h)/(ah^(2)+a^(3)+ah^(2)) = (ah)/(a^(2)+2h^(2)) " " (2)`
From (1) and (2), we have
`m_(1)m_(2) = -1`
` " or " AF bot BE`
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.1|23 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.2|4 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

Let A B C be a triangle with incenter I and inradius rdot Let D ,E ,a n dF be the feet of the perpendiculars from I to the sides B C ,C A ,a n dA B , respectively. If r_1,r_2a n dr_3 are the radii of circles inscribed in the quadrilaterals A F I E ,B D I F ,a n dC E I D , respectively, prove that (r_1)/(r-1_1)+(r_2)/(r-r_2)+(r_3)/(r-r_3)=(r_1r_2r_3)/((r-r_1)(r-r_2)(r-r_3))

O A B C is regular tetrahedron in which D is the circumcentre of O A B and E is the midpoint of edge A Cdot Prove that D E is equal to half the edge of tetrahedron.

D , E ,a n dF are the middle points of the sides of the triangle A B C , then centroid of the triangle D E F is the same as that of A B C orthocenter of the tirangle D E F is the circumcentre of A B C orthocenter of the triangle D E F is the incenter of A B C centroid of the triangle D E F is not the same as that of A B Cdot

In a scalene triangle A B C ,D is a point on the side A B such that C D^2=A D D B , sin s in A S in B=sin^2C/2 then prove that CD is internal bisector of /_Cdot

Let A B C be a triangle. Let A be the point (1,2),y=x be the perpendicular bisector of A B , and x-2y+1=0 be the angle bisector of /_C . If the equation of B C is given by a x+b y-5=0 , then the value of a+b is (a) 1 (b) 2 (c) 3 (d) 4

Let A B C be a given isosceles triangle with A B=A C . Sides A Ba n dA C are extended up to Ea n dF , respectively, such that B ExC F=A B^2dot Prove that the line E F always passes through a fixed point.

If A B C D is quadrilateral and Ea n dF are the mid-points of A Ca n dB D respectively, prove that vec A B+ vec A D + vec C B + vec C D =4 vec E Fdot

Let A B C D be a quadrilateral with area 18 , side A B parallel to the side C D ,a n dA B=2C D . Let A D be perpendicular to A Ba n dC D . If a circle is drawn inside the quadrilateral A B C D touching all the sides, then its radius is 3 (b) 2 (c) 3/2 (d) 1

In Delta ABC , with angle B=90^(@) , BC=6 cm and AB=8 cm, D is a point on AC such that AD=2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.

The mean of a, b, c, d and e is 28. If the mean of a, c and e is 24, then mean of b and d is