Home
Class 12
MATHS
A diagonal of rhombus A B C D is member ...

A diagonal of rhombus `A B C D` is member of both the families of lines `(x+y-1)+lambda1(2x+3y-2)=0`and `(x-y+2)+lambda2(2x-3y+5)=0` and rhombus is (3, 2). If the area of the rhombus is `12sqrt(5)` sq. units, then find the remaining vertices of the rhombus.

Text Solution

Verified by Experts


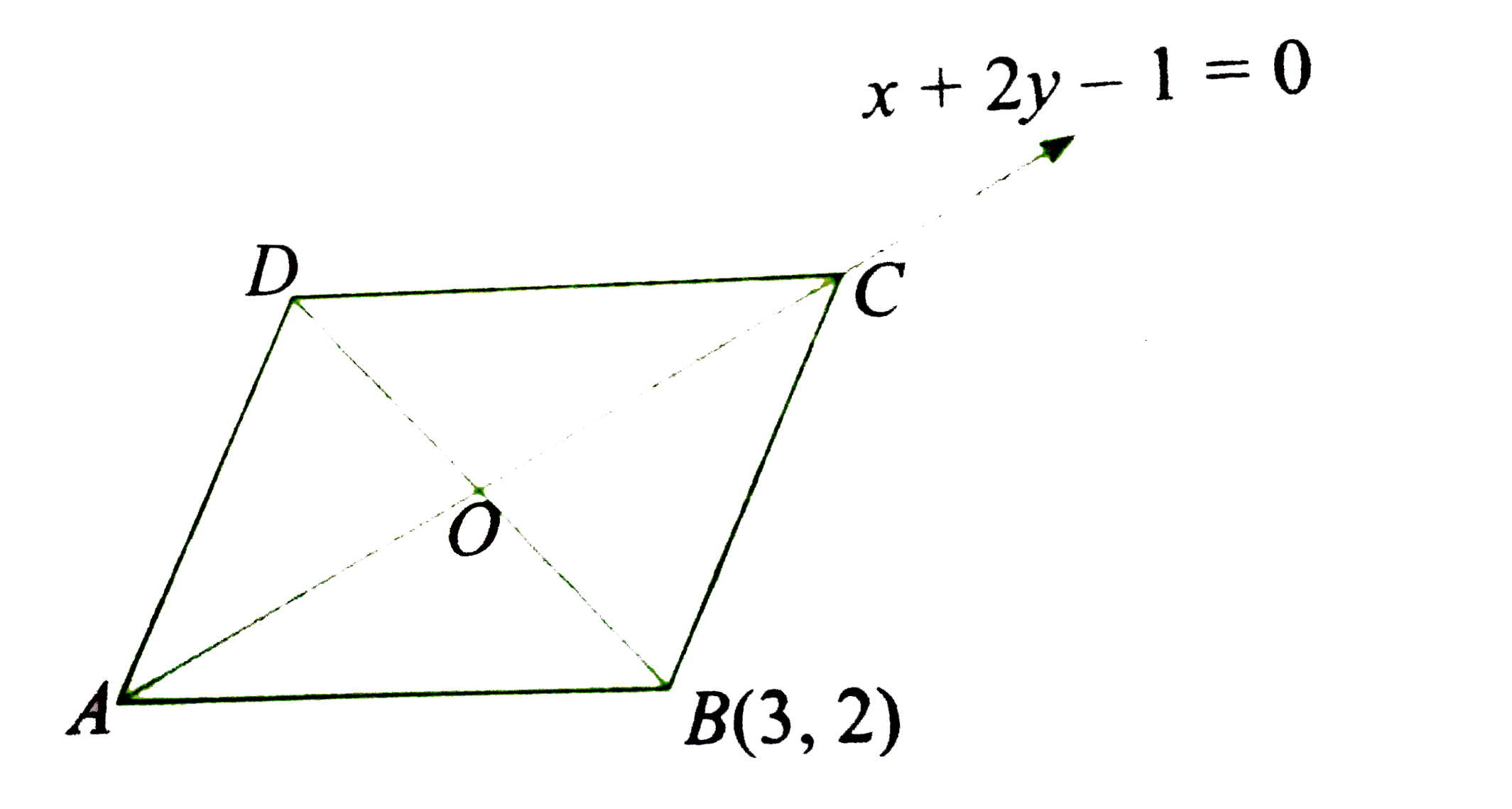
Since diagonal is member of both the given families of line, it will pass through the points (1,0) and (-1,1) which are points where given family of lines are concurrent.
So, equation of diagonal AC is x+2y-1=0.
Clearly, point (3,2) does not satisfy this diagonal.
`therefore "Let" B -= (3,2).`
Diagonal BD is perpendicular to AC.
So, equation of diagonal BD is 2x-y-4=0.
Point of intersection of diagonal AC and BD is O `((9)/(5), (-2)/(5)).`
Since O is midpoint of BD, D `-=((3)/(5),-(14)/(5)).`
`"Now", OD = (6)/(sqrt(5)). So, BD = (12)/(sqrt(5))=d_(1)`
`"Area of rhombus " =(1)/(2)d_(1) xx d_(2) = 12sqrt(5) " " ("where " d_(2) " is length of diagonal AC")`
`therefore d_(2) = 10 " units"`
This is the length of diagonal AC.
Slope of AC `=-(1)/(2) = "tan" theta, "where" theta` is inclination of AC with x-axis.
Since OA=OC=5, using parametic from of straight line, we have
`A,C -= ((9)/(5)+-5"cos" theta, -(2)/(5) +- 5 "sin" theta)`
`-= ((9)/(5)+-5(-(2)/(sqrt(5))), -(2)/(5) +- 5 ((1)/(sqrt(5))))`
`-= ((9)/(5)-2sqrt(5), -(2)/(5) + sqrt(5)), ((9)/(5)+2sqrt(5), -(2)/(5) - sqrt(5))`
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.1|23 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.2|4 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

Consider the family of lines 5x+3y-2+lambda_(1)(3x-y-4)=0 " and " x-y+1+lambda_(2)(2x-y-2)=0 . Find the equation of a straight line that belongs to both the families.

If the two sides of rhombus are x+2y+2=0 and 2x+y-3=0, then find the slope of the longer diagonal.

Two sides of a rhombus lying in the first quadrant are given by 3x-4y=0a n d12 x-5y=0 . If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.

The equation of straight line belonging to both the families of lines (x-y+1)+lambda_1(2x-y-2)=0 and (5x+3y-2)+lambda_2(3x-y-4)=0 where lambda_1, lambda_2 are arbitrary numbers is (A) 5x -2y -7=0 (B) 2x+ 5y - 7= 0 (C) 5x + 2y -7 =0 (D) 2x- 5y- 7= 0

If the equation of any two diagonals of a regular pentagon belongs to the family of lines (1+2lambda)y-(2+lambda)x+1-lambda=0 and their lengths are sin 36^0 , then the locus of the center of circle circumscribing the given pentagon (the triangles formed by these diagonals with the sides of pentagon have no side common) is (a) x^2+y^2-2x-2y+1+sin^2 72^0=0 (b) x^2+y^2-2x-2y+cos^2 72^0=0 (c) x^2+y^2-2x-2y+1+cos^2 72^0=0 (d) x^2+y^2-2x-2y+sin^2 72^0=0

Find the area of a triangle formed by lines 3x+y-2=0, 5x+2y-3=0 and 2x-y-3=0

The diagonals A C and B D of a rhombus intersect at (5,6)dot If A-=(3,2), then find the equation of diagonal B Ddot

If one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units

If the lines 3x^(2)-4xy +y^(2) +8x - 2y- 3 = 0 and 2x - 3y +lambda = 0 are concurrent, then the value of lambda is

If (-4,7) is one vertex of a rhombus and if the equation of one diagonal is 5x - y + 7 =0 , then find the equation of another diagonal.