Let `A B C` be a given isosceles triangle with `A B=A C` . Sides `A Ba n dA C` are extended up to `Ea n dF ,` respectively, such that `B ExC F=A B^2dot` Prove that the line `E F` always passes through a fixed point.

Explanation

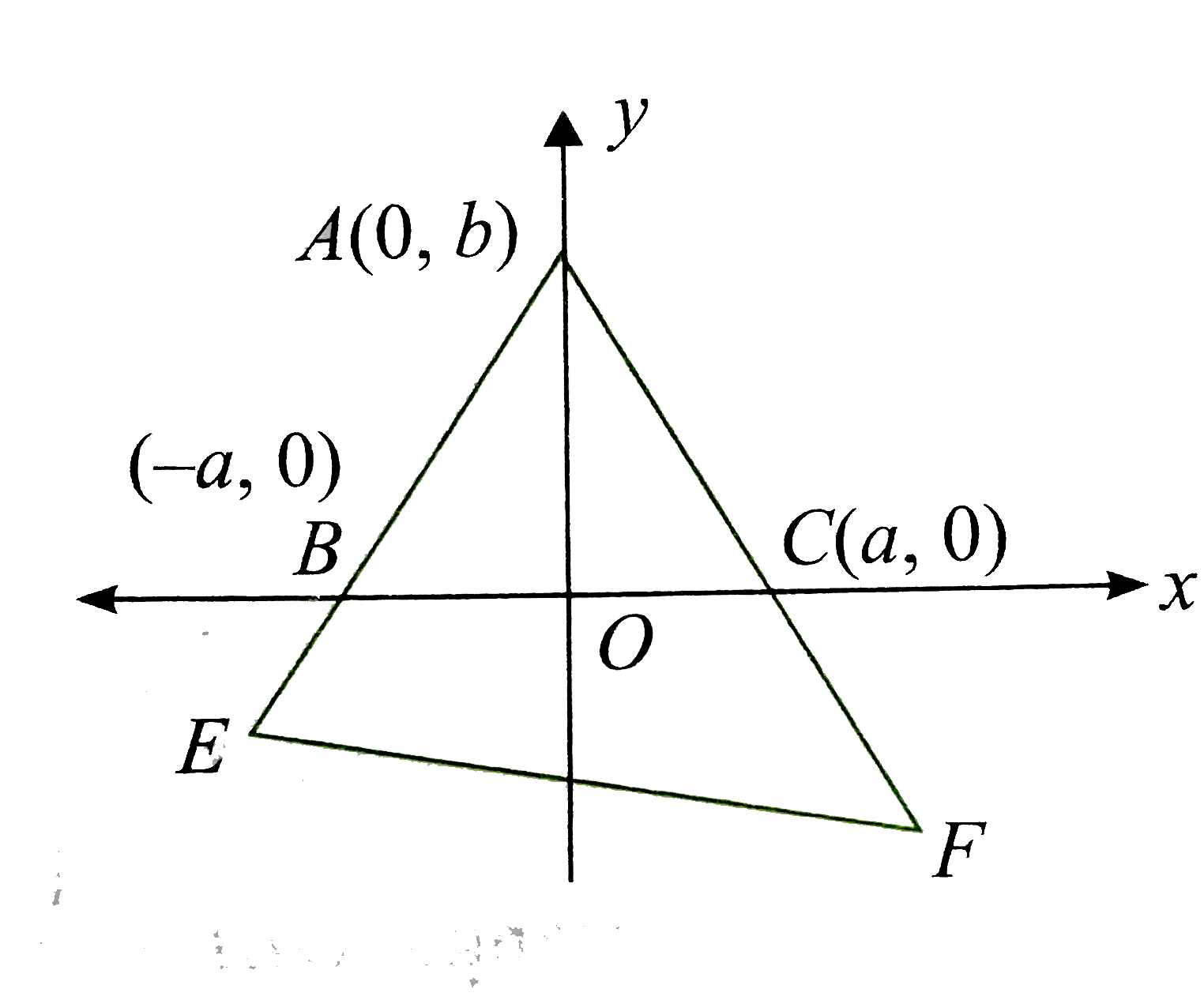
Let ABC be the triangle having vertices (-a,0), (0,b), and (a,0), Now,
`BE xx CF = AB^(2)`
`" or " (BE)/(AB) = (AB)/(CF) = lambda ("Let")`
`" or " (BE)/(AB) = (AC)/(CF) = lambda`
Hence, the coordinates of E and F are `(-a(lambda+1), -lambdab) " and " (a(1+1//lambda), -b//lambda).`The equation of line EF is
`y+lambdab = (-lambdab+(b)/(lambda))/(-a(lambda+1)-(a(lambda+1))/(lambda)) = [x+a(lambda+1)]`
`" or " y+lambda b = ((b)/(lambda)(1-lambda^(2)))/(-(a(lambda+1))/(lambda)[1+lambda]) = [x+a(lambda+1)]`
`" or " y+lambda b = (b(lambda-1))/(a(lambda+1))[x+a(lambda+1)]`
`" or " a(lambda+1)y+ablambda(lambda+1) = b(lambda-1)x+ab(lambda^(2)-1)`
` "or " (bx+ay+ab)-lambda(bx-ay-ab)=0`
which is the equation of a family of lines passing through the point of intersection of the lines bx+ay+ab=0 and bx-ay-ab=0, the point of intersection being (0,-6). Hence, the line EF passes through a fixed point.