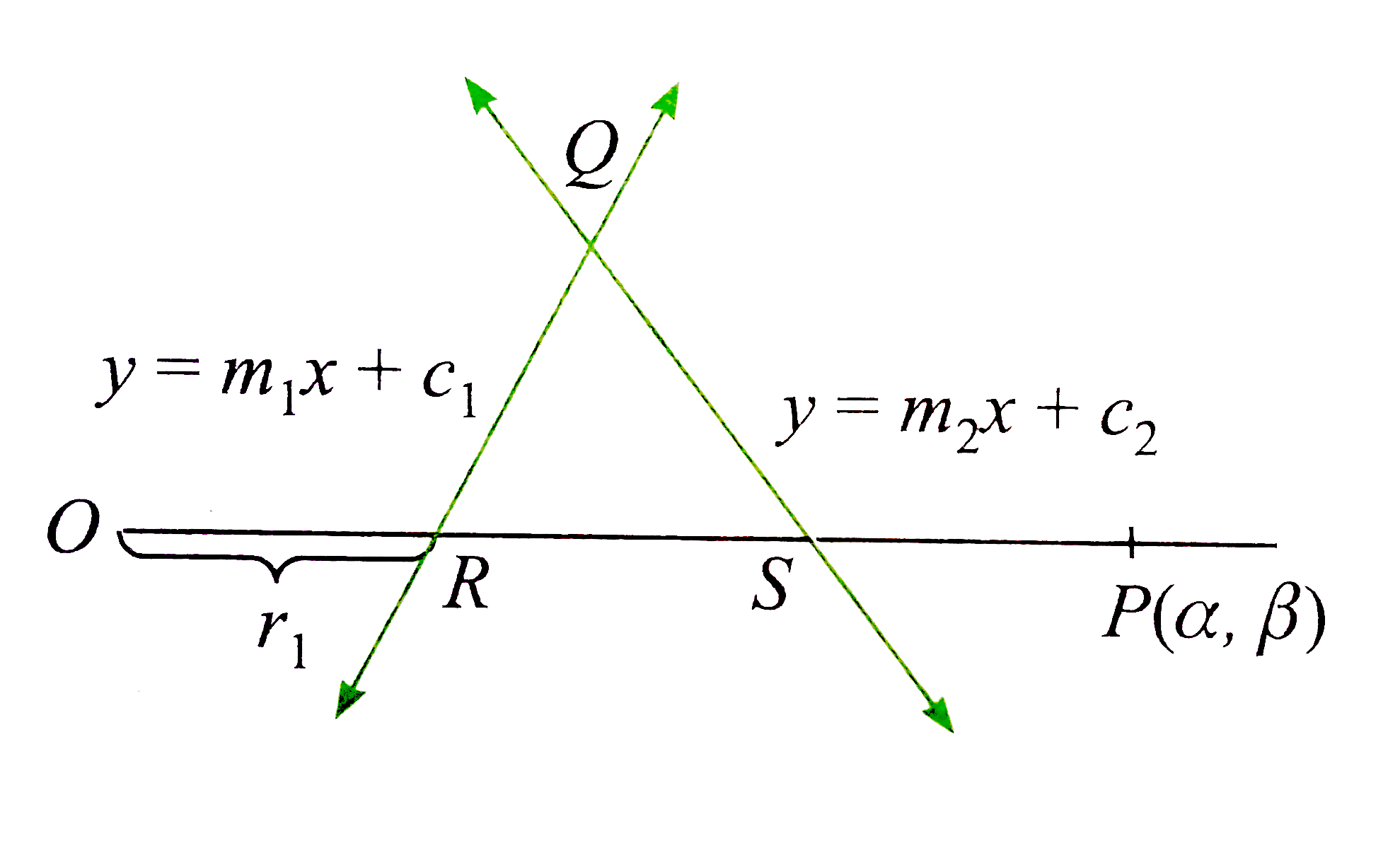
Let the variable line through O makes an angle `theta` with the positive direction of the x-axis. Any point on this variable line is `(O+ r "cos" theta, 0+r"sin" theta)`
`i.e., (r"cos" theta, r"sin" theta)`
Let the fixed lines be
`y=m_(1)x+c_(1) " " (1)`
`"and " y=m_(2)x+c_(2) " " (2)`
`"Let " OR = r_(1), OS=r_(2), OP =r_(3).` So, according to the equation,
`(m+n)/(r_(3)) = (m)/(r_(1))+(m)/(r_(2)) " " (3)`
Since R and S lie on lines (1) and (2), respectively, we have
`r_(1) "sin" theta = m_(1) (r_(1) "cos" theta)+c_(1) " " (4)`
`"and " r_(2) "sin" theta = m_(2) (r_(2) "cos" theta)+c_(2) " " (5)`
` "Let" P-= (alpha, beta). " Then",`
`alpha =r_(3) "cos" theta, beta = r_(3) "sin" theta " " (6)`
From (3), (4), and (5), we have
`(m+n)/(r_(3)) = m ("sin" theta-m_(1) "cos" theta)/(c_(1)) = +n("sin" theta-m_(2) "cos" theta)/(c_(2))` ltrgt `" or " m+n=(m)/(c_(1)) (beta-m_(1)alpha)+ (n)/(c_(2))(beta-m_(2)alpha) " " [From (6)]`
Hence, the locus of P is
` m+n=((m)/(c_(1)) + (n)/(c_(2)))y-((mm_(1))/(c_(1)) + (nm_(2))/(c_(2)))x`
`"or " y-m_(1)x-c_(1)+(n)/(m)(c_(1))/(c_(2))(y-m_(2)x-c_(2))=0 " " (7)`
Clearly, the locus of P is a straight line passing through the point of intersection of the given lines (1) and (2).