Home
Class 12
MATHS
The equations of the perpendicular bisec...

The equations of the perpendicular bisectors of the sides `A Ba n dA C` of triangle `A B C` are `x-y+5=0` and `x+2y=0` , respectively. If the point `A` is `(1,-2)` , then find the equation of the line `B Cdot`

Text Solution

Verified by Experts

The correct Answer is:
14x+23y-40=0

Since the given lines are perpendicular bisectors of the sides as shown in the figure, point B and C are the images of the point A in these lines. Therefore,
`(x_(1)-1)/(1) = (y_(1)-2)/(2) = -(2(1-4))/(1+4)`
`"and " (x_(2)-1)/(1) = (y_(2)+2)/(-1) = -(2(1+2+5))/(1+1)`
`therefore B(x_(1), y_(1))-= (11//5, 2//5) " and " C(x_(2), y_(2))-= (-7,6)`
Hence, the line passing through the points B and C is 14x+23y-40=0.
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.6|5 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise (Single)|82 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.4|8 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

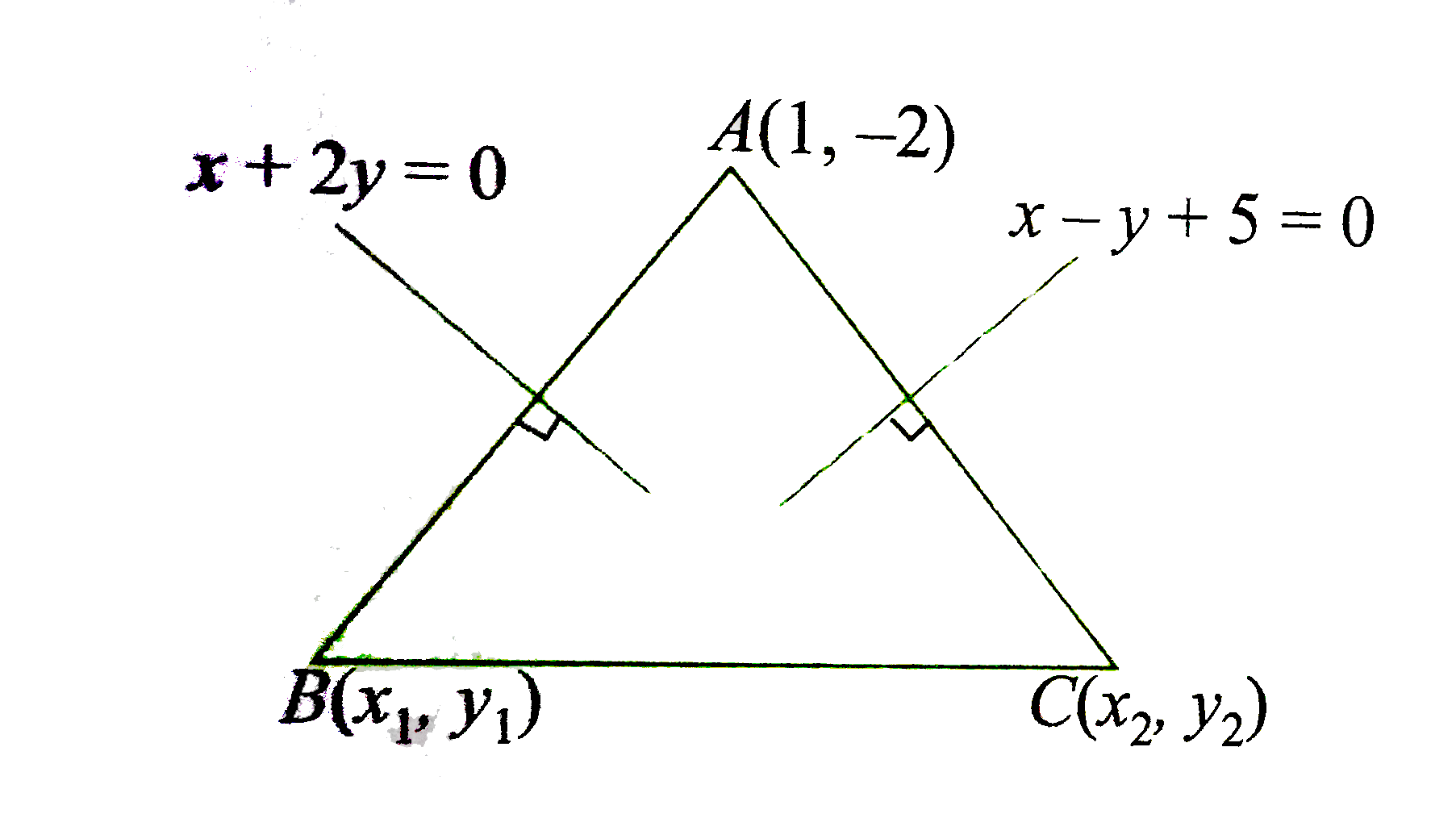
In triangle A B C , the equation of the right bisectors of the sides A B and A C are x+y=0 and y-x=0 , respectively. If A-=(5,7) , then find the equation of side B Cdot

If the middle points of the sides B C ,C A , and A B of triangle A B C are (1,3),(5,7), and (-5,7), respectively, then find the equation of the side A Bdot

In a triangle A B C , side A B has equation 2x+3y=29 and side A C has equation x+2y=16. If the midpoint of B C is (5, 6), then find the equation of B Cdot

Line x + 2y - 8 = 0 is the perpendicular bisector of AB. If B = (3, 5) the A is

Orthocenter and circumcenter of a "Delta"A B C are (a , b)a n d(c , d) , respectively. If the coordinates of the vertex A are (x_1,y_1), then find the coordinates of the middle point of B Cdot

The equations of two equal sides A Ba n dA C of an isosceles triangle A B C are x+y=5 and 7x-y=3 , respectively. Then the equation of side B C if a r( A B C)=5u n i t^2 is x-3y+1=0 (b) x-3y-21=0 3x+y+2=0 (d) 3x+y-12=0

In an isosceles triangle ABC, the coordinates of the points B and C on the base BC are respectively (1, 2) and (2. 1). If the equation of the line AB is y= 2x, then the equation of the line AC is

The equations of the sides of a triangle are x+y-5=0, x-y+1=0, and y-1=0. Then the coordinates of the circumcenter are

Find the equation of the bisectors of the anglebetween the lines 4x+3y=5 and x +2y+3=0.

Find the equations of the bisector of the acute angle between the lines 3x + 4y + 2 = 0 and 5x + 12y - 5 = 0 .