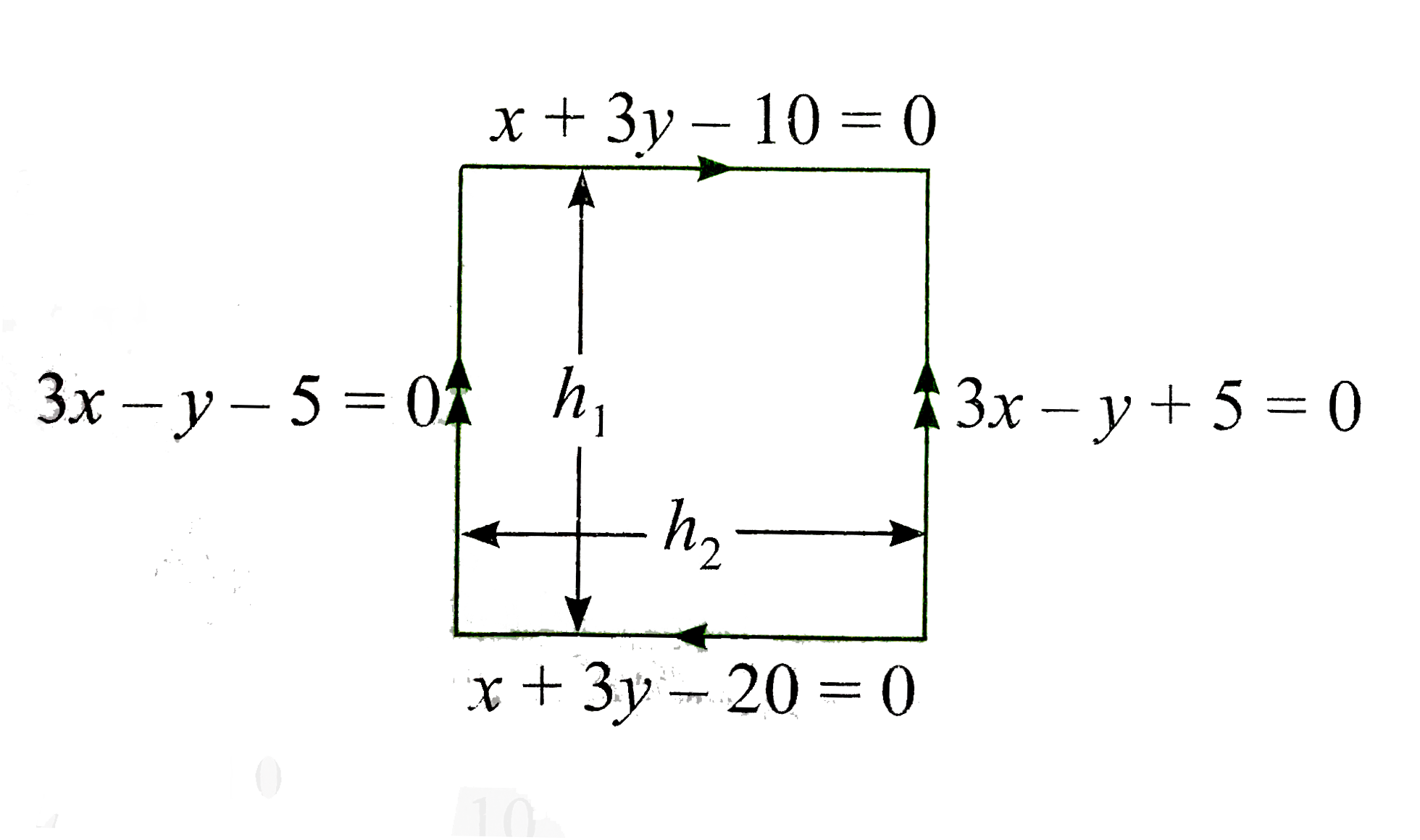Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRAIGHT LINES
CENGAGE|Exercise Exercise (Numerical)|13 VideosSTRAIGHT LINES
CENGAGE|Exercise JEE Main Previous Year|9 VideosSTRAIGHT LINES
CENGAGE|Exercise Exercise (Comprehension)|27 VideosSTRAIGHT LINE
CENGAGE|Exercise Multiple Correct Answers Type|8 VideosTHEORY OF EQUATIONS
CENGAGE|Exercise JEE Advanced Previous Year|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-STRAIGHT LINES-Exercise (Matrix)
- Consider the lines represented by equation (x^(2) + xy -x) xx (x-y) =0...
Text Solution
|
- Consider the triangle formed by the lines y+3x+2=0, 3y-2x-5=0, 4y+x...
Text Solution
|
- A straight line with negative slope passing the point (1, 4) meets the...
Text Solution
|
- If the point P is symmetric to the point Q(4,-1) with respect to the ...
Text Solution
|
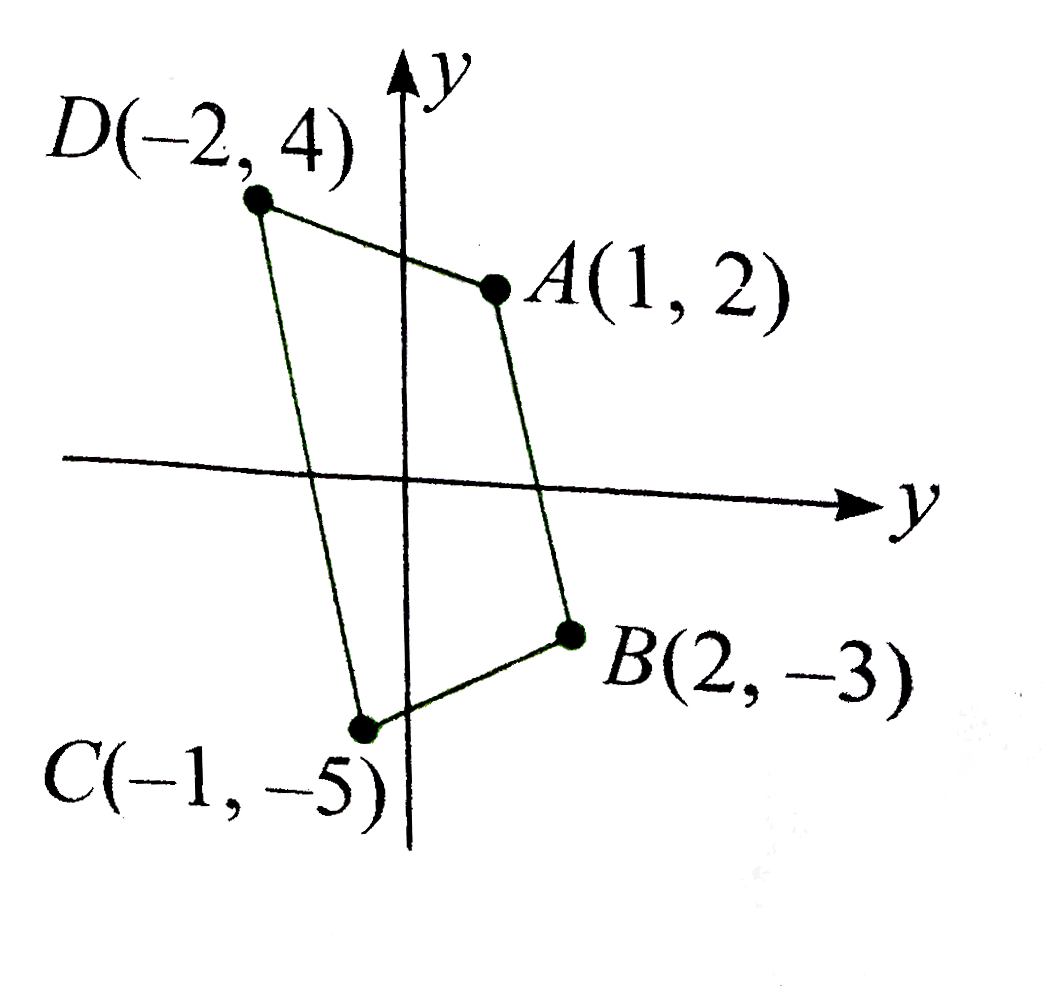
- The point A(1,2), B(2,-3), C(-1,-5) and D(-2, 4) in order are the vert...
Text Solution
|
- Differentiate y = sin(x^2 + 3).
Text Solution
|
- Consider the lines given by L(1):x+3y-5=0 L(2):3x-ky-1=0 L(3):5x...
Text Solution
|
- Consider a DeltaABC in which sides AB and AC are perpendicular to x-y...
Text Solution
|