Home
Class 12
MATHS
Consider a DeltaABC whose sides AB, BC a...

Consider a `DeltaABC` whose sides `AB, BC and CA` are represented by the straight lines `2x + y=0, x + py =q and x -y= 3` respectively. The point P is `(2,3)`. If P is orthocentre,then find the value of (p+q) is

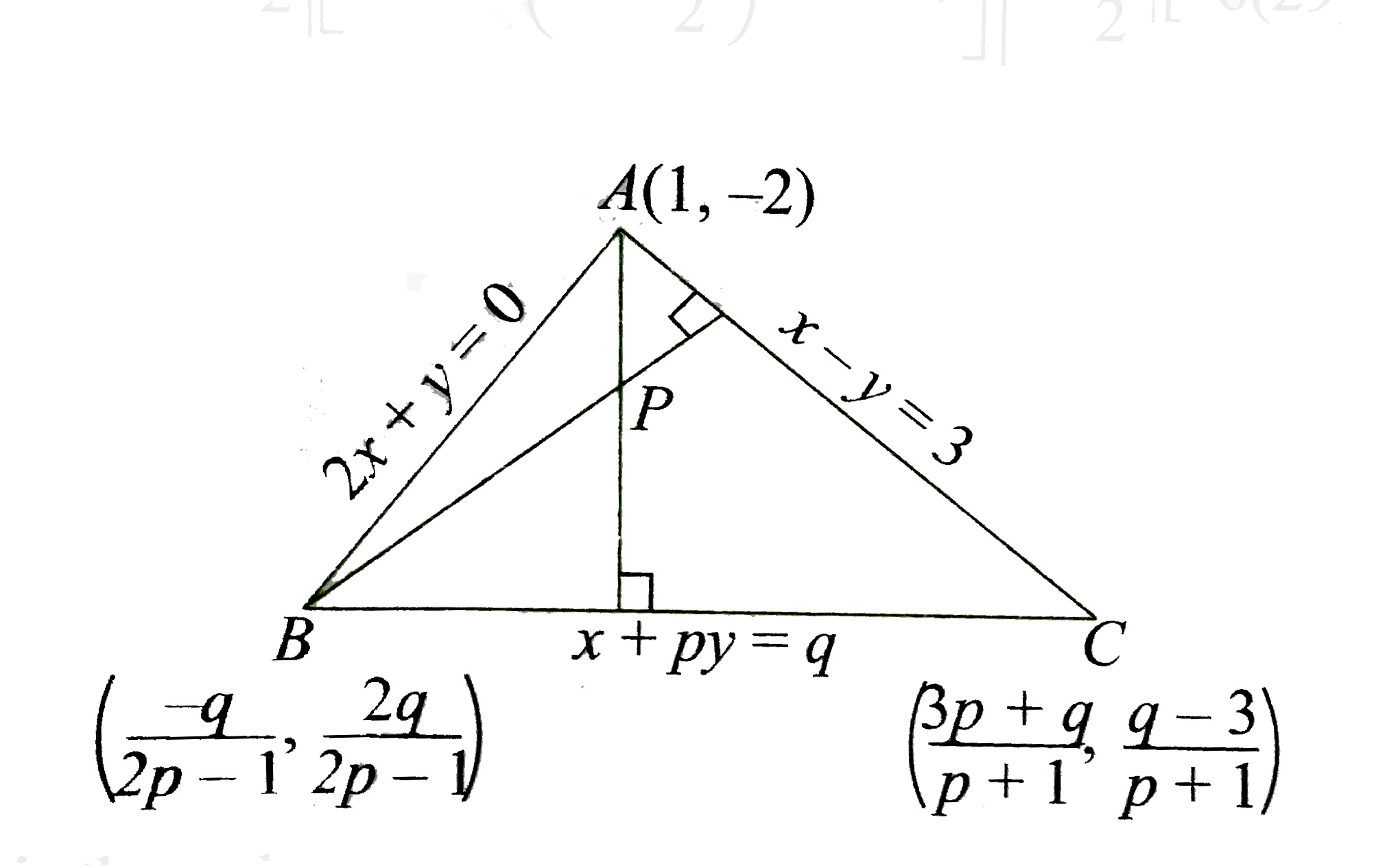
Text Solution

Verified by Experts

The correct Answer is:
50

P is the orthocenter. Therefore,
`AP bot BC`
`"or " (-(1)/(p))((3+2)/(2-1)) = -1`
`"or " (5)/(p)= 1 " or " p =5`
Since `BP bot AC`, we have
`(27-2q)/(18+q) = -1`
or q =27+18
or q = 45
`therefore p+q=5+45=50`
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise JEE Main Previous Year|9 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise JEE Advanced Previous Year|4 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise (Matrix)|8 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

Consider a DeltaABC in which sides AB and AC are perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of DeltaABC is (3/2, 5/2). The equation of the line in List I is of the form ax+by+c=0, where a,b,c in I. Match it with the corresponding value of c in list II and then choose the correct code. Codes : {:(a, b, c, d),(r, s, p, q),(s, r, q, p),(q, p, s, r),(r, p, s, q):}

If the straight lines y/2=x-p and ax+5=3y are parallel , then find "a" .

If the straight lines 12y=-(p+3)x+12, 12x-7y=16 are perpendicular then find 'p'.

A line intersects the straight lines 5x-y-4=0 and 3x-4y-4=0 at A and B , respectively. If a point P(1,5) on the line A B is such that A P: P B=2:1 (internally), find point Adot

A straight line through the origin 'O' meets the parallel lines 4x +2y= 9 and 2x +y=-6 at points P and Q respectively. Then the point 'O' divides the segment PQ in the ratio

If the straight lines 12y=-(p+3)x+12,12x-7y=16 are perpendicular find 'p' .

Find the value of p so that the three lines 3x + y - 2 = 0, px + 2y - 3 = 0 " and " 2x - y - 3 = 0 may intersect at one point.

If the equation p x^2+(2-q)x y+3y^2-6q x+30 y+6q=0 represents a circle, then find the values of pa n dqdot

P and Q trisect the line segment joining the points (2,1) and (5,-8) . If the point P lies on 2x-y+k=0, then find the value of k.