Home
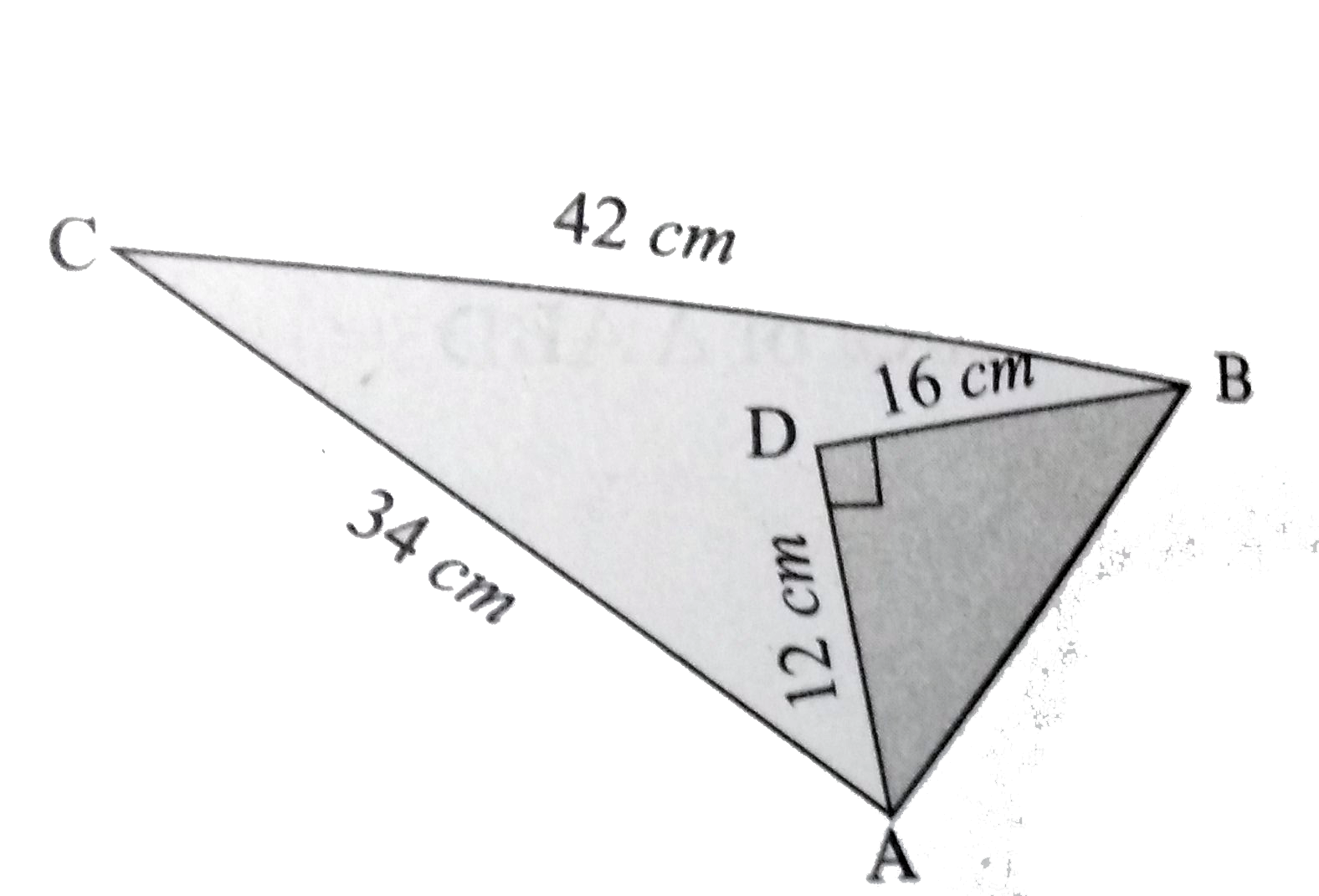
Class 12
MATHS
Find the area of the unshaded region....

Find the area of the unshaded region.

A

`PrarrIV, QrarrII, R rarrI,SrarrIII`

B

`PrarrIV,QrarrIII,R rarrI, SrarrII`

C

`PrarrIV,QrarrI,R rarrIII, SrarrII`

D

`PrarrIII, QrarrIV,R rarrII, S rarrI`

Text Solution

Verified by Experts

The correct Answer is:
B

`" Area of " DeltaLMN=4sqrt3`
`(1)/(2)(2b)(sqrt3b)=4sqrt3`
`rArr" "b^(2)=4rArrb=2rArr2b=4`
Here, `(a)/(b)=cot 30^(@)rArra=sqrt3b rArra=2sqrt3`
Now, `b^(2)=a^(2)(e^(2)-1)`
`therefore" "4=12(e^(2)-1)`
`rArr" "e^(2)=1+(1)/(3)=(4)/(3)`
`rArr" "e=(2)/(sqrt3)`
`"Distance between foci"=2ae=2xx2sqrt3xx(2)/(sqrt3)=8`
`"Lenght of latus rectum "=(2b^(2))/(a)=(2xx4)/(2sqrt3)=(4)/(sqrt3)`
Promotional Banner

Topper's Solved these Questions

  • HYPERBOLA

    CENGAGE|Exercise JEE Main Previous Year|3 Videos

  • HIGHT AND DISTANCE

    CENGAGE|Exercise JEE Previous Year|3 Videos

  • INDEFINITE INTEGRATION

    CENGAGE|Exercise Question Bank|21 Videos

Similar Questions

Explore conceptually related problems

Find the area of the shaded region.

Using the above figure (a).Find the equation of AB. (b) Find the point P. (c) Find the area of the shaded region by integration.

Consider the functions, f(x) = |x| - 1 and g(x) = 1 - |x| (a) Sketch their graphs and shade the closed region between them. (b) Find the area of their shaded region.

The following figure represents the circle x^(2) + y^(2) = 4 and the curve y = |x| Find the area of the shaded region using integration.

(i) Draw a rough sketch of the curve y^(2) = x and shade the region bounded by the line x = 1 and the curve. (ii) Using integration find the area of the shaded region.

Find the area of the smaller region bounded by the ellipse (x^(2))/(a^(2)) + (y^(2))/(b^(2)) = 1 and the line (x)/(a) + (y)/(b) = 1 .

Find the area of the smaller region bounded by the ellipse (x^(2))/(9) + (y^(2))/(4) = 1 and the line (x)/(3) + (y)/(2) = 1

Find the area of the region bounded by y^2=4ax and x=|y| .

Find the area of the region bounded by the parabola y = x^(2) and y = |x| .