Home
Class 12
MATHS
Given that P(3,1),Q(6. 5), and R(x , y) ...

Given that `P(3,1),Q(6. 5),` and `R(x , y)` are three points such that the angle `P R Q` is a right angle and the area of ` R Q P` is 7, find the number of such points `Rdot`

Text Solution

Verified by Experts

Clearly, R lies on the circle with P and Q as end points of diameter.

Now, `PQ=sqrt((6-3)^2+(5-1)^2)=5`
`therfore` Radius, `r=2.5`
Now, area of triangle `PQR=(1/2)RM.PQ=7`
`rArrRm=(14)/(5)=2.8`,
which is not possible as RM cannot be more than radius Hence, no such triangle is possible.
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSYEM

    CENGAGE|Exercise Exercise 1.1|6 Videos

  • COORDINATE SYSYEM

    CENGAGE|Exercise Exercise 1.2|8 Videos

  • COORDINATE SYSTEM

    CENGAGE|Exercise Multiple Correct Answers Type|2 Videos

  • CROSS PRODUCTS

    CENGAGE|Exercise DPP 2.2|13 Videos

Similar Questions

Explore conceptually related problems

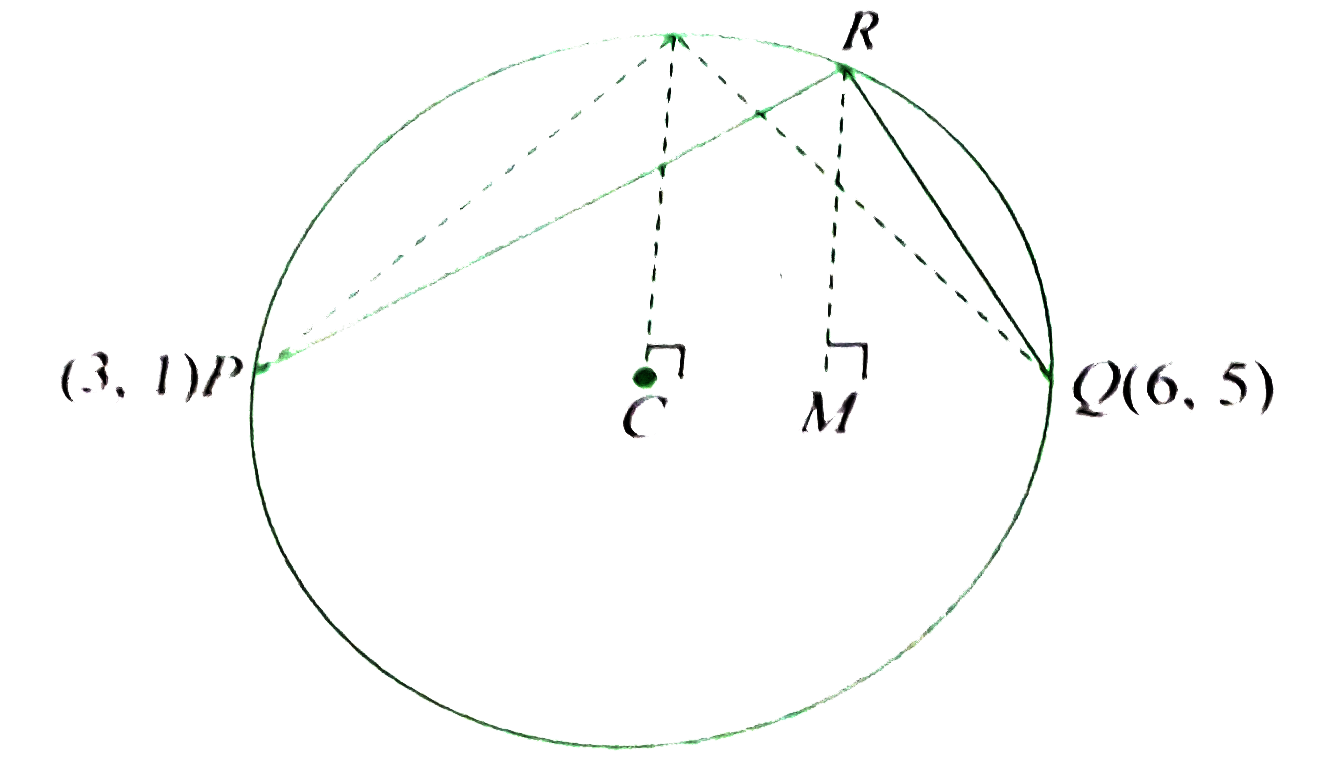
Given that P(3,1),Q(6. 5), and R(x , y) are three points such that the angle P Q R is a right angle and the area of R Q P is 7, find the number of such points Rdot

Let P=(-1, 0), Q=(0,0) and R=(3, 3sqrt3 ) be three points. The equation of the bisector of the angle PQR is

Two points P(a,0) and Q(-a,0) are given. R is a variable point on one side of the line P Q such that /_R P Q-/_R Q P is a positive constant 2alphadot Find the locus of the point Rdot

If from a point P , tangents P Qa n dP R are drawn to the ellipse (x^2)/2+y^2=1 so that the equation of Q R is x+3y=1, then find the coordinates of Pdot

Let P be (5,3) and a point R on y = x and Q on the X - axis be such that PQ +QR+RP is minimum ,then the coordinates of Q are

P is a point on the line y+2x=1, and Q and R two points on the line 3y+6x=6 such that triangle P Q R is an equilateral triangle. The length of the side of the triangle is (a) 2/(sqrt(5)) (b) 3/(sqrt(5)) (c) 4/(sqrt(5)) (d) none of these

Let O(0,0),P(3,4), and Q(6,0) be the vertices of triangle O P Q . The point R inside the triangle O P Q is such that the triangles O P R ,P Q R ,O Q R are of equal area. The coordinates of R are (a) (4/3,3) (b) (3,2/3) (c) (3,4/3) (d) (4/3,2/3)

If p,q and r are simple propositions such that (p^^q)^^(q^^r) is true, then

Find the points of contact Q and R of a tangent from the point P(2,3) on the parabola y^2=4xdot