Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-COORDINATE SYSYEM -Exercise 1.2
- The distance between the points (a cos alpha, a sin alpha) and (a cos...
Text Solution
|
- If X ={-5,1,3,4} and Y={a,b,c} , then which of the following relations...
Text Solution
|
- If the points (1,1):(0,sec^2theta); and (cos e c^2theta,0) are coll...
Text Solution
|
- If the area of the circle is A1 and the area of the regular pentagon i...
Text Solution
|
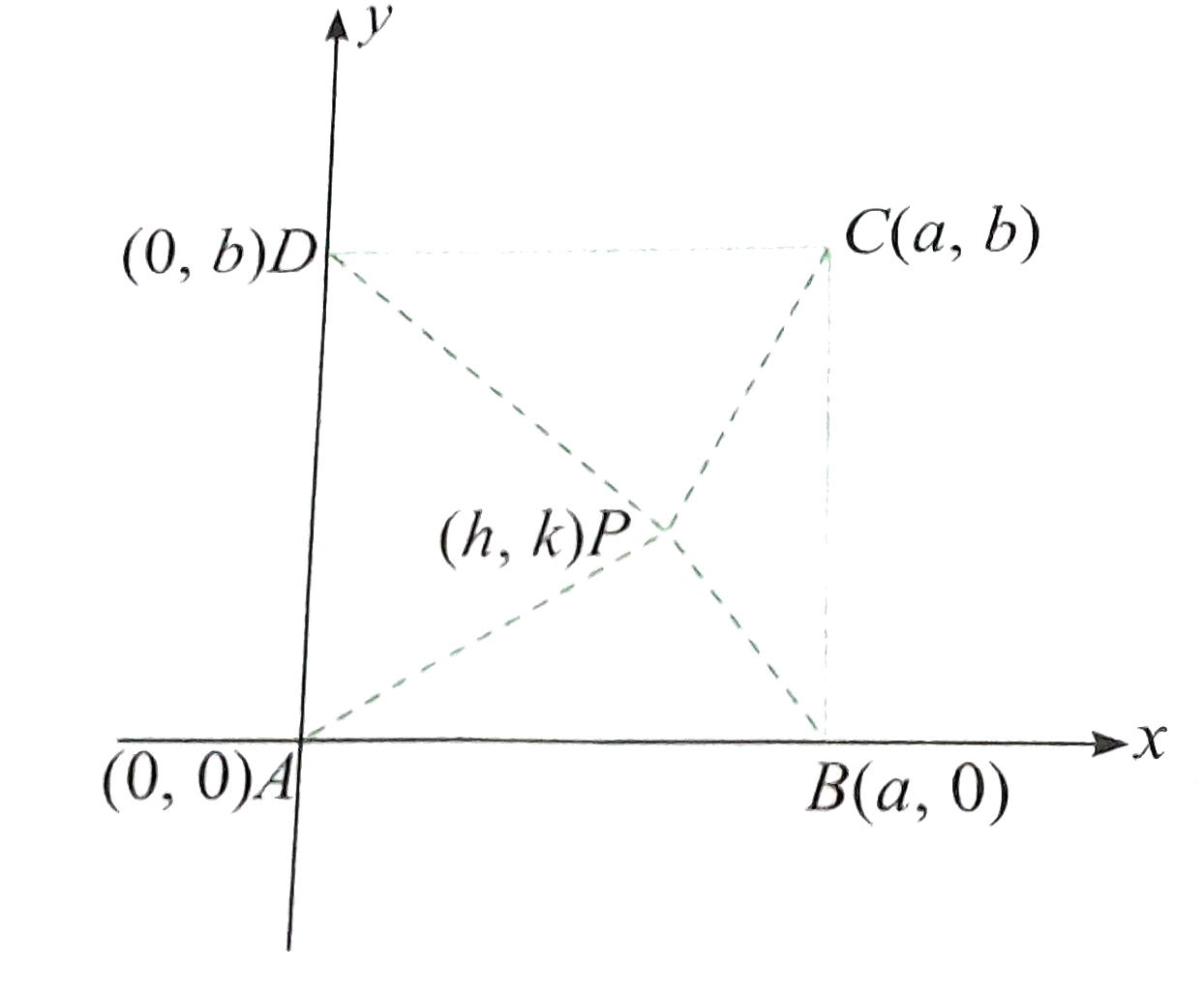
- Let A B C D be a rectangle and P be any point in its plane. Show that ...
Text Solution
|
- Find the length of altitude through A of the triangle A B C , where...
Text Solution
|
- Find the area of the pentagon whose vertices are A(1,1),B(7,21),C(7,-3...
Text Solution
|
- Four points A(6,3),B(-3,5),C(4,-2) and D(x ,2x) are given in such a...
Text Solution
|