Home
Class 12
MATHS
A man starts from the point P(-3,4) and ...

A man starts from the point `P(-3,4)` and reaches the point `Q(0,1)` touching the x-axis at `R(alpha,0)` such that `PR+RQ` is minimum. Then `alpha` and `|alpha|`.

Text Solution

Verified by Experts

The correct Answer is:
0.6
For PR=RQ to be minimum,it should be the path of light.

`therefore anglePRA=angleQRM`
From similar triangles PAR and QMR.
`(AR)/(RM)=(PA)/(QM)`
or `(alpha+3)/(0-alpha)=(4)/(1)or alpha=-(3)/(5)`
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSYEM

    CENGAGE|Exercise JEE Main Previous Year|6 Videos

  • COORDINATE SYSYEM

    CENGAGE|Exercise Exercise (Matrix)|4 Videos

  • COORDINATE SYSTEM

    CENGAGE|Exercise Multiple Correct Answers Type|2 Videos

  • CROSS PRODUCTS

    CENGAGE|Exercise DPP 2.2|13 Videos

Similar Questions

Explore conceptually related problems

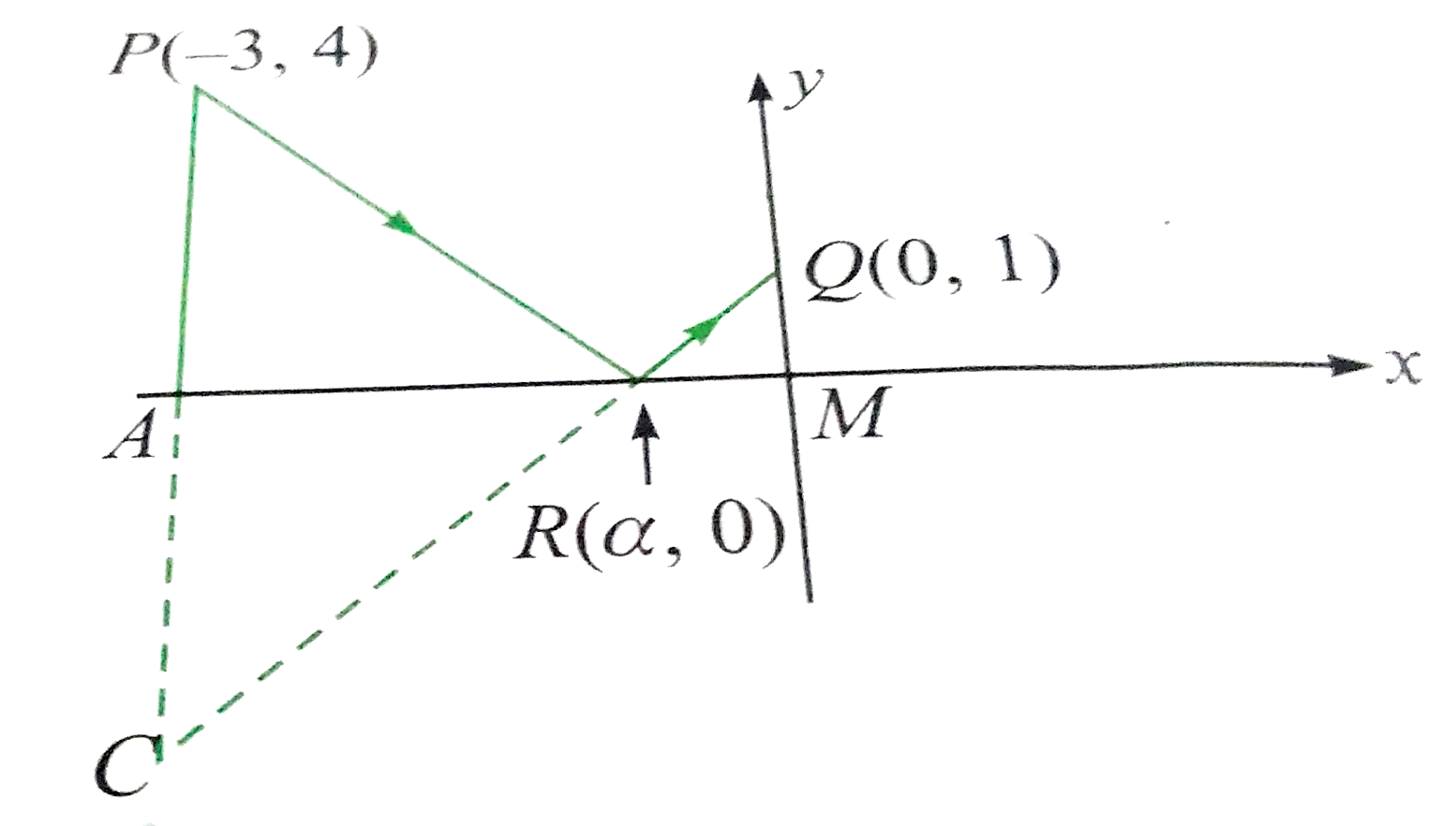
A man starts from the point P(-3,4) and reaches the point Q(0,1) touching the x-axis at R(alpha,0) such that P R+R Q is minimum. Then 5|alpha| (A) 3 (B) 5 (C) 4 (D) 2

If two distinct tangents can be drawn from the Point (alpha,2) on different branches of the hyperbola x^2/9-y^2/(16)=1 then (1) |alpha| lt 3/2 (2) |alpha| gt 2/3 (3) |alpha| gt 3 (4) alpha =1

sin 3 alpha = 4 sin alpha sin(x + alpha) sin(x-alpha)

In R^(3) , consider the planes P_(1):y=0 and P_(2),x+z=1. Let P_(3) be a plane, different from P_(1) and P_(2) which passes through the intersection of P_(1) and P_(2) , If the distance of the point (0,1,0) from P_(3) is 1 and the distance of a point (alpha,beta,gamma) from P_(3) is 2, then which of the following relation(s) is/are true?

If the line ax+ by =1 passes through the point of intersection of y =x tan alpha + p sec alpha, y sin(30^@-alpha)-x cos (30^@-alpha) =p , and is inclined at 30^@ with y=tan alpha x , then prove that a^2 + b^2 = 3/(4p^2) .

If alpha" and "beta are the roots of the quadratic equation 4x^(2)+3x+7=0 , then the value of (1)/(alpha)+(1)/(beta)=

If alpha, beta are the roots of x^(2) - px + q = 0 and alpha', beta' are the roots of x^(2) - p' x + q' = 0 , then the value of (alpha - alpha')^(2) + (beta + alpha')^(2) + (alpha - beta')^(2) + (beta - beta')^(2) is

The circle x^2+y^2=4 cuts the line joining the points A(1, 0) and B(3, 4) in two points P and Q . Let BP/PA=alpha and BQ/QA=beta . Then alpha and beta are roots of the quadratic equation

If alpha and beta are the roots of the equation x^(2)-ax+b=0 ,find Q(b) (1)/(alpha)+(1)/(beta)

Three normals with slopes m_1, m_2 and m_3 are down from a point P not on the axis of the axis of the parabola y^2 = 4x . If m_1 m_2 = alpha , results in the locus of P being a part of parabola, Find the value of alpha