Home
Class 12
MATHS
Complex numbers z(1) and z(2) satisfy |z...

Complex numbers `z_(1)` and `z_(2)` satisfy `|z_(1)|=2` and `|z_(2)|=3`. If the included angle of their corresponding vectors is `60^(@)`, then the value of `19|(z_(1)-z_(2))/(z_(1)+z_(2))|^(2)` is

A

`5`

B

`6`

C

`7`

D

`8`

Text Solution

Verified by Experts

The correct Answer is:
C
`(c )`
`OC=|z_(1)+z_(2)|` and `AB=|z_(1)-z_(2)|`
`|z_(1)+z_(2)|=sqrt(|z_(1)|^(2)+|z_(2)|^(2)-2|z_(1)||z_(2)|cos120^(@))`
`=sqrt(4+9+2.3)=sqrt(19)`
and `|z_(1)-z_(2)|=sqrt(|z_(1)|^(2)+|z_(2)|^(2)-2|z_(1)||z_(2)|cos60^(@))`
`=sqrt(4+9-6)=sqrt(7)`
`:.|(z_(1)-z_(2))/(z_(1)+z_(2))|=sqrt((7)/(19))`
`:.19|(z_(1)-z_(2))/(z_(1)+z_(2))|^(2)=7`
Promotional Banner

Topper's Solved these Questions

  • COMPLEX NUMBERS

    CENGAGE|Exercise Multiple Correct Answer|11 Videos

  • COMPLEX NUMBERS

    CENGAGE|Exercise Matching Column|1 Videos

  • CIRCLES

    CENGAGE|Exercise Question Bank|16 Videos

  • CONIC SECTIONS

    CENGAGE|Exercise Solved Examples And Exercises|87 Videos

Similar Questions

Explore conceptually related problems

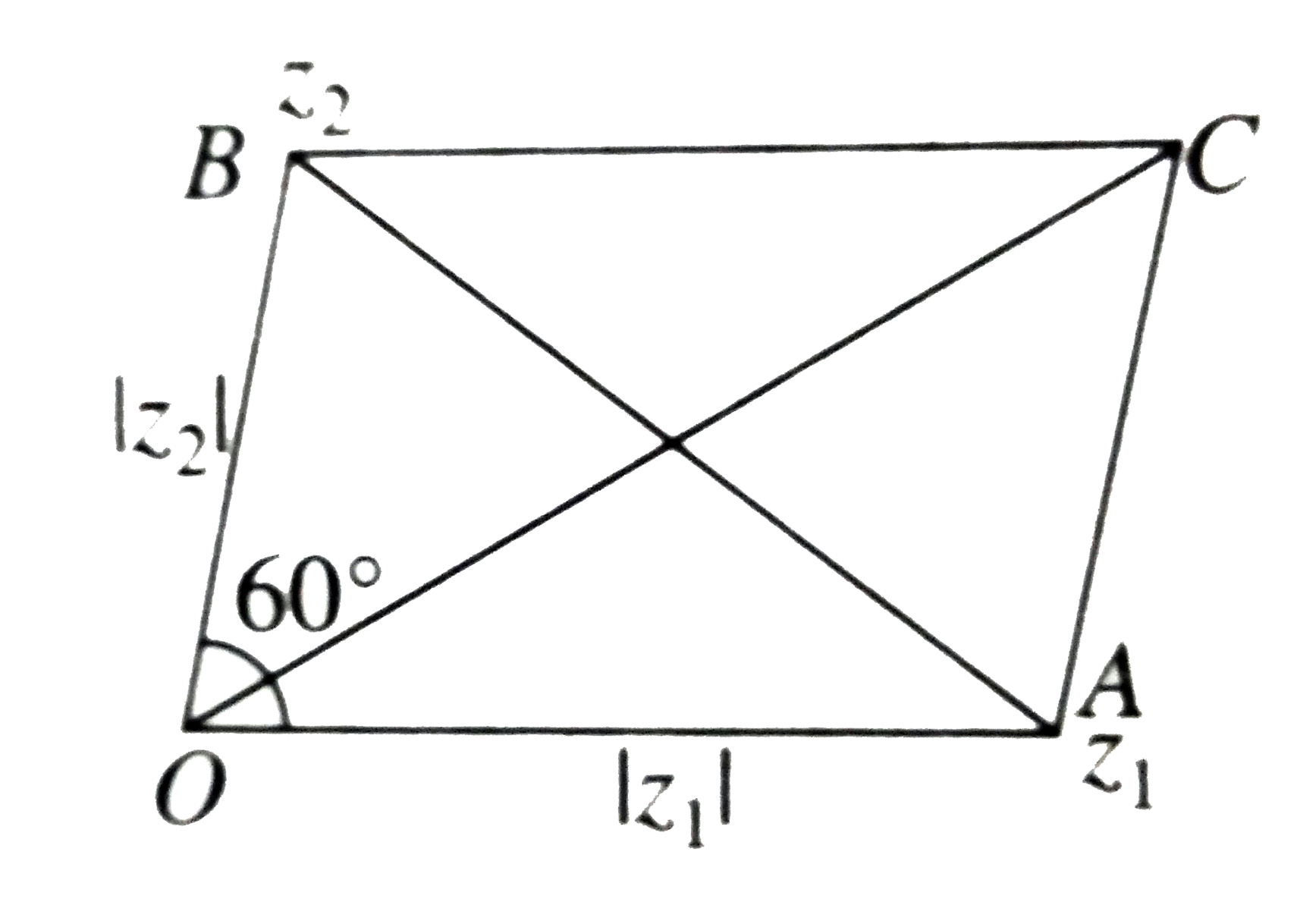
It is given that complex numbers z_1a n dz_2s a t i sfy|z_1|=22a n d|z_2|=3. If the included angled of their corresponding vectors is 60^0 , then find the value of |(z_1+z_2)/(z_1-z_2)| .

For all complex numbers z_1,z_2 satisfying |z_1|=12 and |z_2-3-4i|=5 , find the minimum value of |z_1-z_2|

If (2z_1)/(3z_2) is purely imaginary then |(z_(1)-z_(2))/(z_(1)+z_(2))|

If z_(1)=2-i, z_(2)=1+i , find |(z_(1)+z_(2)+1)/(z_(1)-z_(2)+1)| .

If z_(1)=4+5i and z_(2)=-3+2i that (z_(1))/(z_(2)) is :

If z_(1)=3-4i , z_(2)=2+i find bar(z_(1)z_(2))

If 2z_1//3z_2 is a purely imaginary number, then find the value of "|"(z_1-z_2")"//(z_1+z_2)|dot

|z_(1)|=|z_(2)|" and "arg z_(1)+argz_(2)=0 then

All complex numbers 'z' which satisfy the relation |z-|z+1||=|z+|z-1|| on the complex plane lie on the