If the area of bounded between the x-axis and the graph of `y=6x-3x^2` between the ordinates `x=1a n dx=a` is `19` units, then `a` can take the value `4or-2` two value are in (2,3) and one in `(-1,0)` two value are in (3,4) and one in `(-2,-1)` none of these

Explanation

We have `y=3x(2-x)`

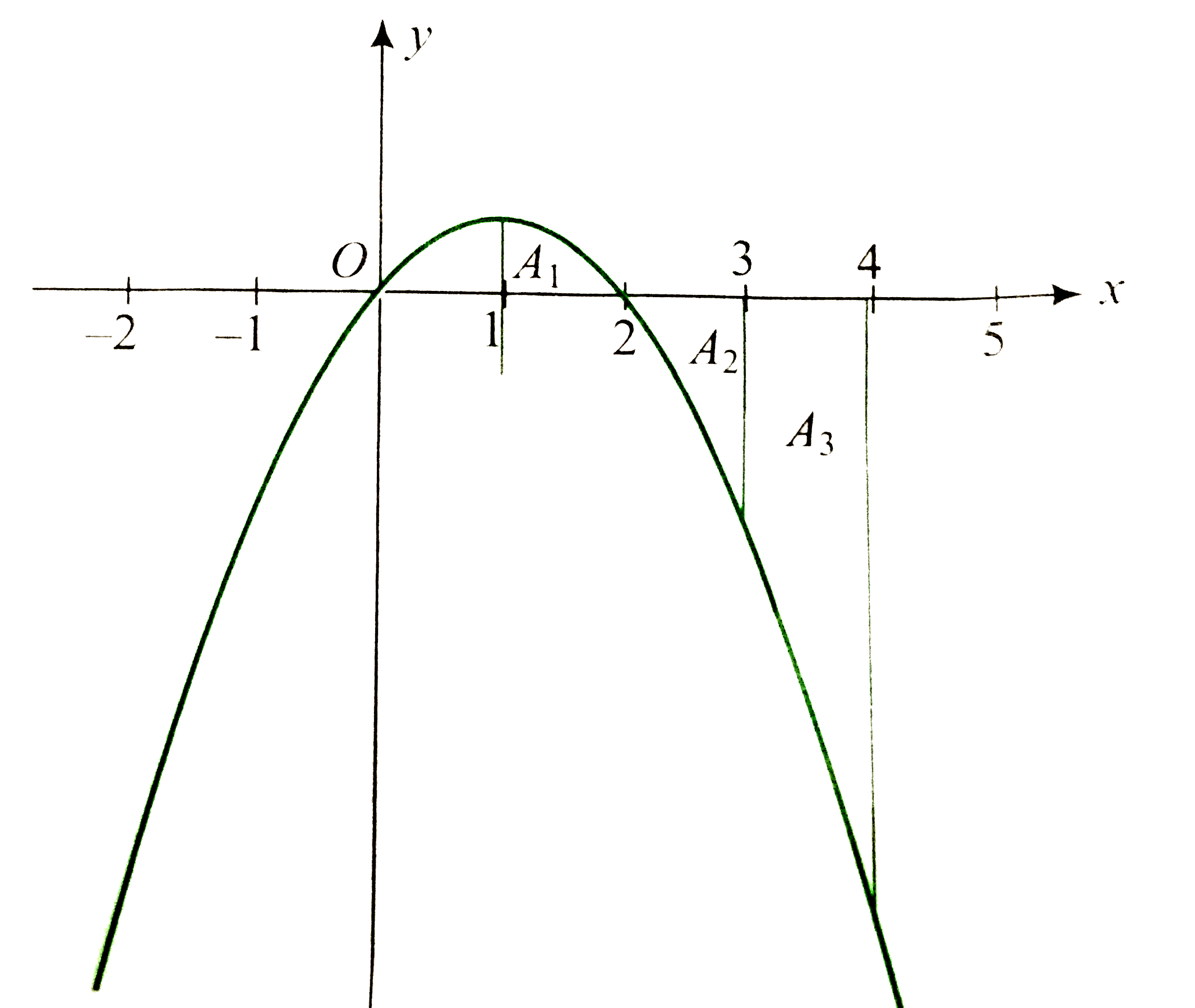
Graph of the function is downward parabola intersecting x-axis at `x=0 and x=2.`
`"Now "I=int(6x-3x^(2))dx=(6x^(2))/(2)-(3x^(3))/(3)`
`3x^(2)-x^(3)`
`x^(2)(3-x)=F(x)`
`"Now "A_(1)=F(2)-F(1)=4-2=2 "sq. units"`
`A_(2)=F(2)-F(3)=4-0=4 " sq. units"`
`A_(3)=F(3)-F(4)=0-(-16)=16 " sq. units"`
`"Since "A_(1)+A_(2)+A_(3)=22" sq. units."`
`So, a in (3,4)`
From the symmetric of the parabola, other value of lies in `(-2,-1)`