Solving the given curves we get
`5x-x^(2)=x`
`therefore" "x^(2)-4x=0`
`rArr" "x=0, 4`
`y=x(5-x)` is parabola which is concave downward and intersecting x-axis at x=0 and x=5.
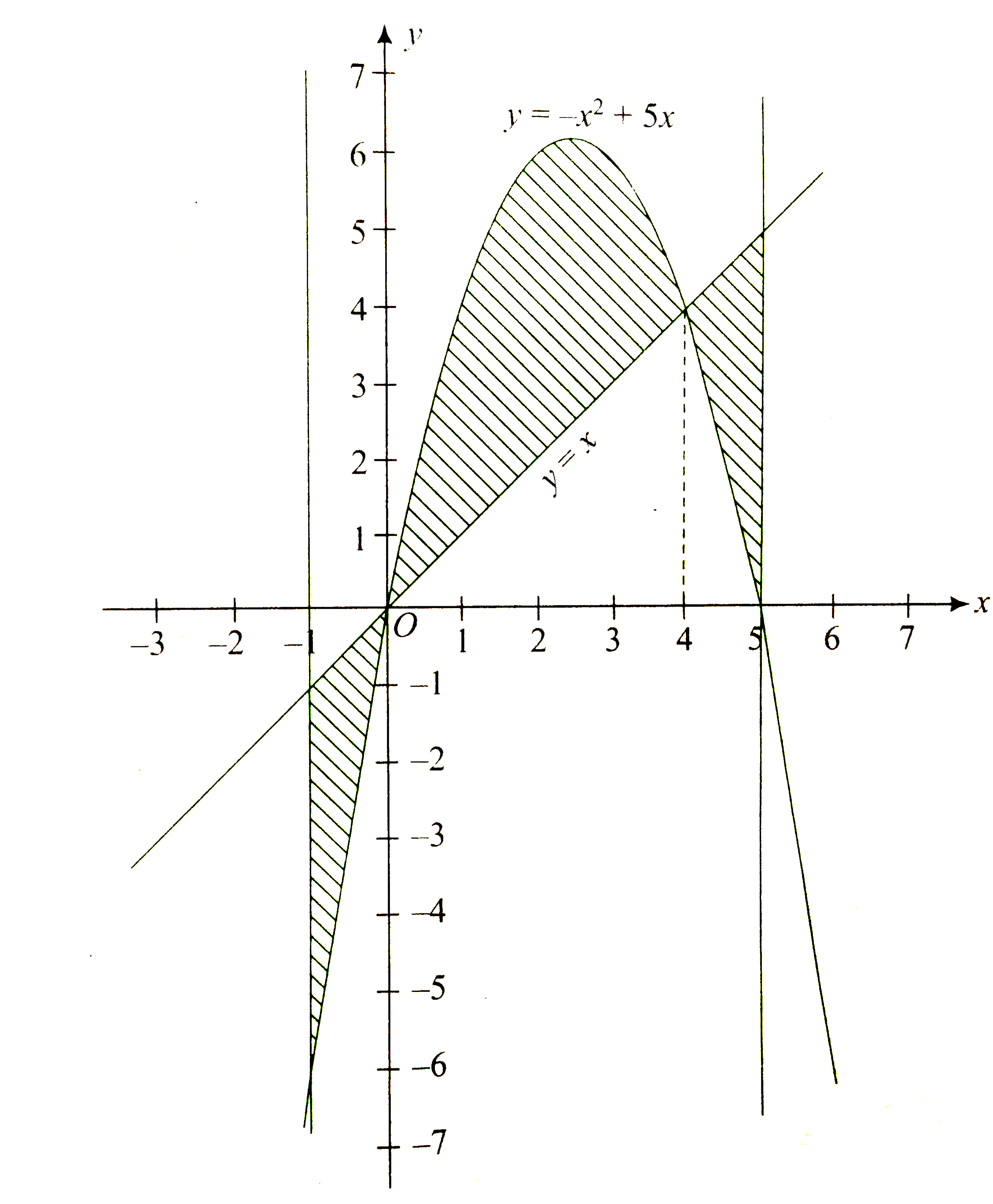
`"Required area, "=overset(5)underset(-1)int|x-(5x-x^(2))|dx`
`=overset(5)underset(-1)int|x-4x|dx`
`=overset(0)underset(-1)int(x^(2)-4x)dx +overset(4)underset(0)int(4x-x^(2))dx+overset(5)underset(4)int(x^(2)-4x)dx`
`=[(x^(3))/(3)-2x^(2)]_(-1)^(0)+[2x^(2)-(x^(3))/(3)]_(0)^(4)+[(x^(3))/(3)-2x^(2)]`
`=-[(-1)/(3)-2]+[32-(64)/(3)]+[(125)/(3)-50]-[(64)/(3)-32]`
`=16-(2)/(3)`
`(46)/(3)` sq. units.