Home
Class 12
MATHS
Let C(1) and C(2) be the graphs of the f...

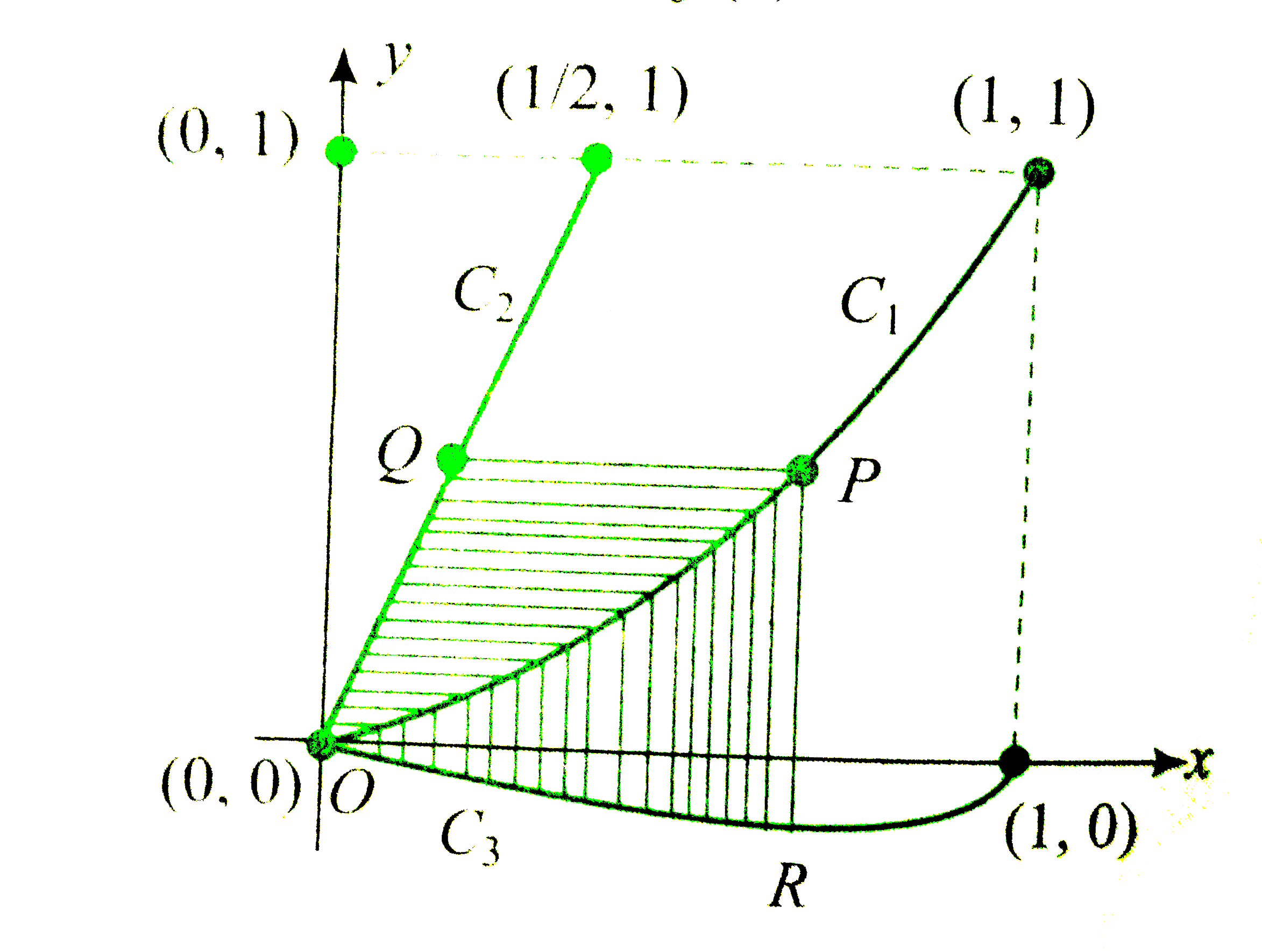
Let `C_(1) and C_(2)` be the graphs of the functions `y=x^(2) and y=2x,` respectively, where `0le x le 1." Let "C_(3)` be the graph of a function y=f(x), where `0lexle1, f(0)=0.` For a point P on `C_(1),` let the lines through P, parallel to the axes, meet `C_(2) and C_(3)` at Q and R, respectively (see figure). If for every position of `P(on C_(1)),` the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

Text Solution

Verified by Experts

Let P be on `C_(1),y=x^(2) be (t,t^(2))`
`therefore" y co-ordinate of Q is also "t^(2)`
`"Now, Q on y =2x where "y=t^(2)`
`therefore" "x=t^(2)//2`
`therefore" "Q((t^(2))/(2),t^(2))`
For point R, x=t and it is on y=f(x)
`therefore" "R(t,f(t))`
Given that,
Area OPQ = Area OPR
`rArr" "int_(0)^(t^(2))(sqrt(y)-(y)/(2))dy=int_(0)^(t)(x^(2)-f(x))dx`
Differentiating both sides w.r.t. t, we get
`(sqrt(t^(2))-(t^(2))/(2))(2t)=t^(2)-f(t)`
`rArr" "f(t)=t^(3)-t^(2)`
`rArr" "f(x)=x^(3)-x^(2)`
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE|Exercise Exercise 9.1|9 Videos

  • AREA

    CENGAGE|Exercise Exercise 9.2|14 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE|Exercise Subjective Type|2 Videos

  • AREA UNDER CURVES

    CENGAGE|Exercise Question Bank|10 Videos

Similar Questions

Explore conceptually related problems

Draw the graph of the function f(x ) = {{:(1+x , -1 le x le 0),( 1-x, 0 lt x le 1):}

Find the area of the region {(x , y): 0 le y le x^(2)+1, 0le y le x +1, 0lex le2}

The range of function y=[x^2]=[x]^2,x in [0,2] (where [.] denotes the greatest function), is {0} b. {0,1} c. {1,2} d. {0,1,2}

Let C_1 and C_2 be two circles whose equations are x^2+y^2-2x=0 and x^2+y^2+2x=0 and P(lambda, lambda) is a variable point

Let f(x) be a polynomial function of second degree. If f(1) = f(-1) and a, b. c are in A.P., then f'(a), f'(b),f'(c) are in

Let f(x)=a sin x+c , where a and c are real numbers and a>0. Then f(x)lt0, AA x in R if

Let C_1 and C_2 be parabolas x^2 = y - 1 and y^2 = x-1 respectively. Let P be any point on C_1 and Q be any point C_2 . Let P_1 and Q_1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P_1 lies on C_2 and Q_1 lies on C_1 and PQ >= [P P_1, Q Q_1] . Hence or otherwise , determine points P_0 and Q_0 on the parabolas C_1 and C_2 respectively such that P_0 Q_0 <= PQ for all pairs of points (P,Q) with P on C_1 and Q on C_2

The following figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L_(1) and L_(2) are parrallel, with L_(1) being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is

Let f(x)=(x^(2)+2)/([x]),1 le x le3 , where [.] is the greatest integer function. Then the least value of f(x) is