Home
Class 12
MATHS
Let O(0,0), A(2,0) and B(1,(1)/(sqrt(3))...

Let O(0,0), A(2,0) and B`(1,(1)/(sqrt(3)))` be the vertices of a triangle Let R be the region consisting of all those point P inside `Delta OAB` which satisfy `d(P, OA) le " min" [d(P,OB),d(P,AB)],` where d denotes the distance from the point to the corresponding line.
Sketch the region R and find its area.

Text Solution

Verified by Experts


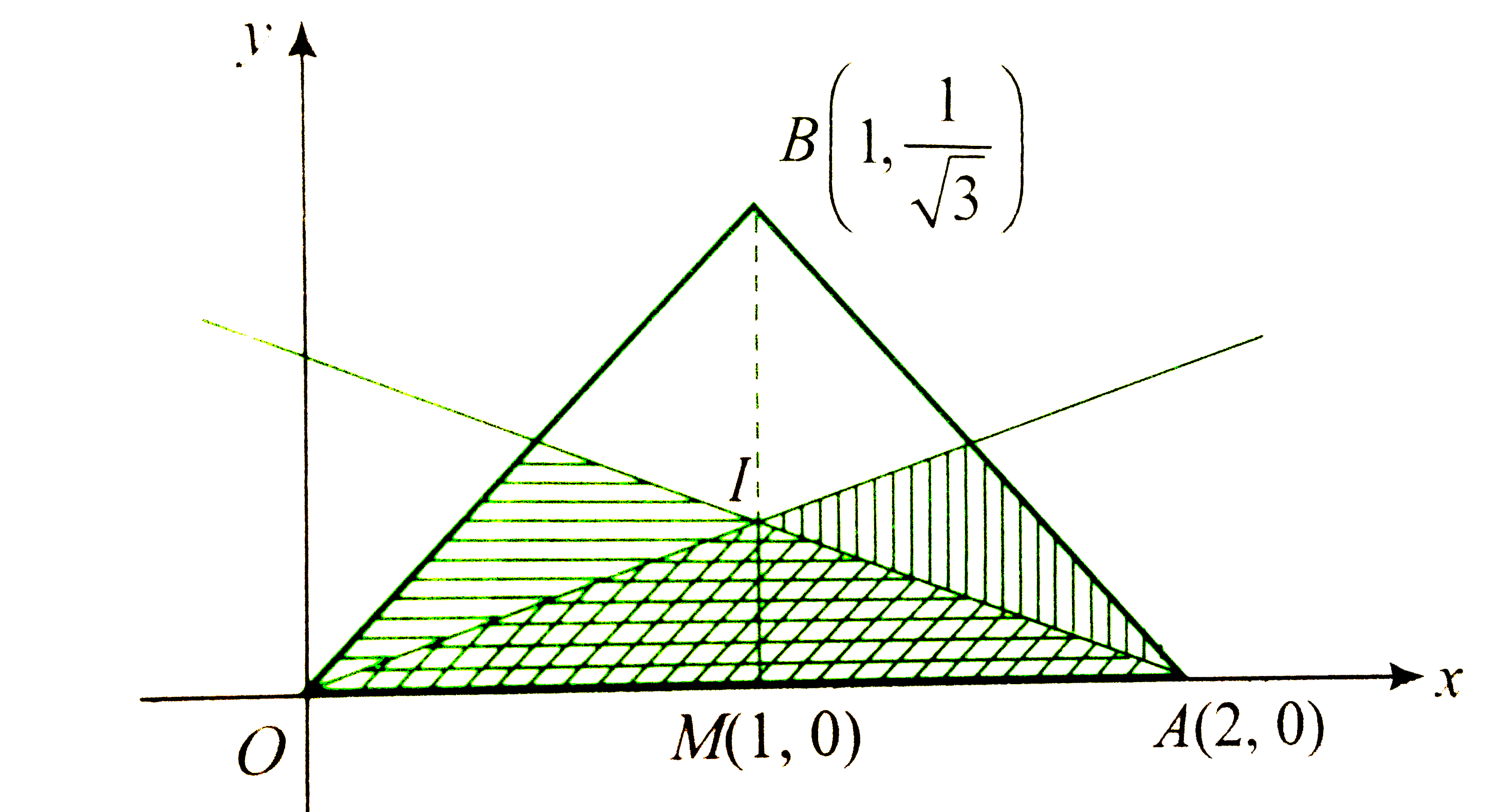
`d(P,OA)le" min "[d(P,OB), d(P,AB)]`
`rArr" "d(P,OA)le d(P,OB) and d(P,OA)led(P,AB)`
When `d(P,OA)=d(P,OB),P` is equidistant from OA and OB, or
P lies on the angular bisector of lines OA and OB.
Hence when `d(P,OA) le d(P,OB),` point P is nearer to OA than to
OB, i.e., lies on or below the bisector of OA and OB.
Similarly, when `d(P,OA)led(P,AB)`, P is nearer to OA then to OB, i.e., lies on or below the bisector of OA and AB.
`therefore" Required area = Area of "Delta OIA.`
`"Now, tan "angleBOA=(1//sqrt(3))/(1)=(1)/(sqrt(3))`
`"or "angleBOA=30^(@)rArrangleIOA=15^(@)`
`rArr" "IM=tan 15^(@)=2-sqrt(3).`
`"Hence, Area of "DeltaOIA =(1)/(2)OAxxIM=(1)/(2)xx2xx(2-sqrt(3))`
`2-sqrt(3)` sq. units.
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE|Exercise Exercise 9.1|9 Videos

  • AREA

    CENGAGE|Exercise Exercise 9.2|14 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE|Exercise Subjective Type|2 Videos

  • AREA UNDER CURVES

    CENGAGE|Exercise Question Bank|10 Videos

Similar Questions

Explore conceptually related problems

Let O be the origin and A be the point (64,0). If P, Q divide OA in the ratio 1:2:3, then the point P is

Let P=(-1, 0), Q=(0,0) and R=(3, 3sqrt3 ) be three points. The equation of the bisector of the angle PQR is

If the points A(6, 1), B(8, 2), C(9, 4) and D(P, 3) are the vertices of a parallelogram, taken in order. Find the value of P.

Find the co-ordinates of all the points P on the ellipse, x^2/a^2+y^2/b^2=1 ,for which the area of the triangle PON is maximum, where O denotes the origin and N, the foot of the perpendicular from O to tangent at P.

Let O(0,0),P(3,4), and Q(6,0) be the vertices of triangle O P Q . The point R inside the triangle O P Q is such that the triangles O P R ,P Q R ,O Q R are of equal area. The coordinates of R are (a) (4/3,3) (b) (3,2/3) (c) (3,4/3) (d) (4/3,2/3)

If the point (0,0),(2,2sqrt(3)), and (P ,q) are the vertices of an equilateral triangle, then (p ,q) is (a) (0,-4) (b) ( 4,4) c)(4,0) (d) (5,0)

In a triangle OAB ,E is the mid point of OB and D is the point on AB such that AD:DB=2:1 If OD and AE intersect at P then determine the ratio of OP: PD using vector methods

Let P(x) denote the probability of the occurrence of event x. Plot all those point (x y) = (P(A), P(B)) in a plane which satisfy the conditions, P(A uu B) ge 3//4 and 1//8 le P(A nn B) le 3//8

Let P denotes the plane consisting of all points that are equidistant from the points A(-4,2,1) and B(2,-4,3) and Q be the plane, x-y+cz=1 where c in R . If the angle between the planes P and Q is 45^(@) then the product of all possible values of c is

Let P denotes the plane consisting of all points that are equidistant from the points A(-4,2,1) and B(2,-4,3) and Q be the plane, x-y+cz=1 where c in R . The planar P is parallel to plane Q