`"We have y"={((1)/(x)-x",",if x in (0,1)),(x-(1)/(x)",", if x gt 1):}`
Graph of the function is as shown in the following figure.
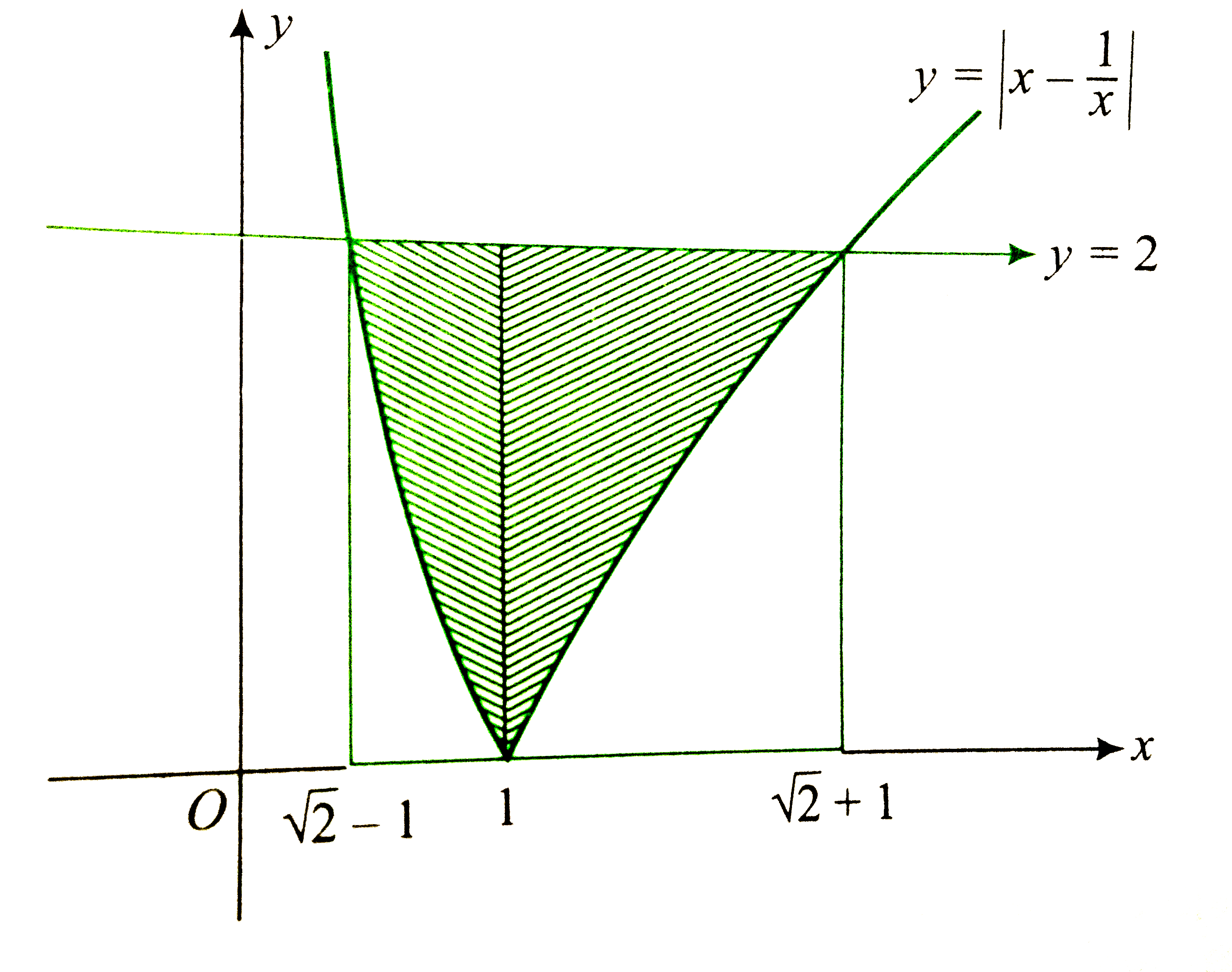
`"Solving "(1)/(x)-x=2, x lt 1,` we get
`x^(2)+2x-1=0`
`therefore" "x=sqrt(2)-1`
`"Solving "x-(1)/(x)=2, x gt1,` we get
`x^(2)-2x-1=0`
`therefore" "x=sqrt(2)+1`
`therefore" "Required area,
A=overset(1)underset(sqrt(2)-1)int(2-((1)/(x)-x))dx +overset(sqrt(2)+1)underset(1)int(2-(x-(1)/(x)))dx`
`=overset(1)underset(sqrt(2)-1)int(2+x-(1)/(x))dx+overset(sqrt(2)+1)underset(1)int(2+(1)/(x)-x)dx`
`=[2x+(x^(2))/(2)-log_(e)x]_(sqrt(2)-1)^(1)+[2x-(x^(2))/(2)+log_(e)x]_(1)^(sqrt(2)+1)`
`=(5)/(2)-(2-sqrt(2)-2+(3-2sqrt(2))/(2)-log_(e)(sqrt(2)-1))+2sqrt(2)+2-(3+2sqrt(2))/(2)+log_(e)(sqrt(2)+1)+(3)/(2)`
`=5+log_(e)(sqrt(2)+1)+log_(e)(sqrt(2)-1)=2`