Equation of curve can be re-written as
`2y^(2)+6(1+x)y+5x^(2)+7x+6=0`
`rArr" "y_(1)=(-3(1+x)-sqrt((3-x)(x-1)))/(2)`
`y_(2)=(-(1+x)+sqrt((3-x)(x-1)))/(2)`
Therefore, the curves `(y_(1) and y_(2))` are defined for values of x for whih `(3-x)(x-1)ge 0,` i.e., `1le x le 3.`
(Actually the given equation represents an ellipse, because `Delta ne 0 and h^(2) lt ab.`)
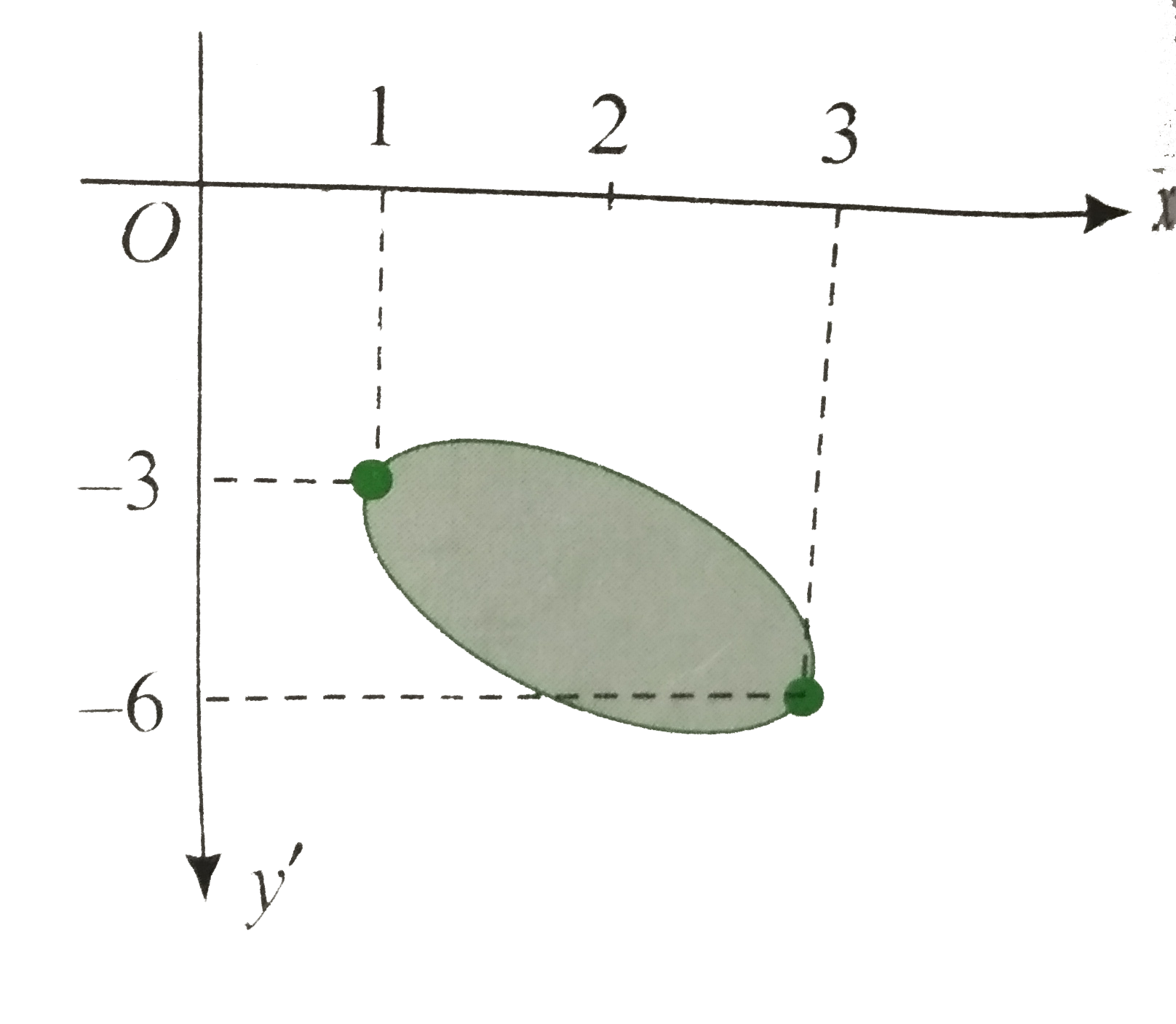
Required are will be given by
`A=overset(3)underset(1)int |y_(1)-y_(2)|dxrArrA=overset(3)underset(1)intsqrt((3-x)(x-1))dx`
`"Put "x=3 cos^(2)theta+ sin^(2)theta, i.e., dx=-2 sin 2theta d""theta`
`therefore" "A=2overset(pi//2)underset(0)intsin^(2) 2theta d""theta =(pi)/(2)` sq. units.