Let `A_n` be the area bounded by the curve `y=(tanx)^n` and the lines `x=0,y=0,` and `x=pi/4dot` Prove that for `n >2,A_n+A_(n-2)=1/(n-1)` and deduce `1/(2n+2)

Explanation

`"We have "A_(n)=int_(0)^(pi//4)(tan x)^(n) dx`

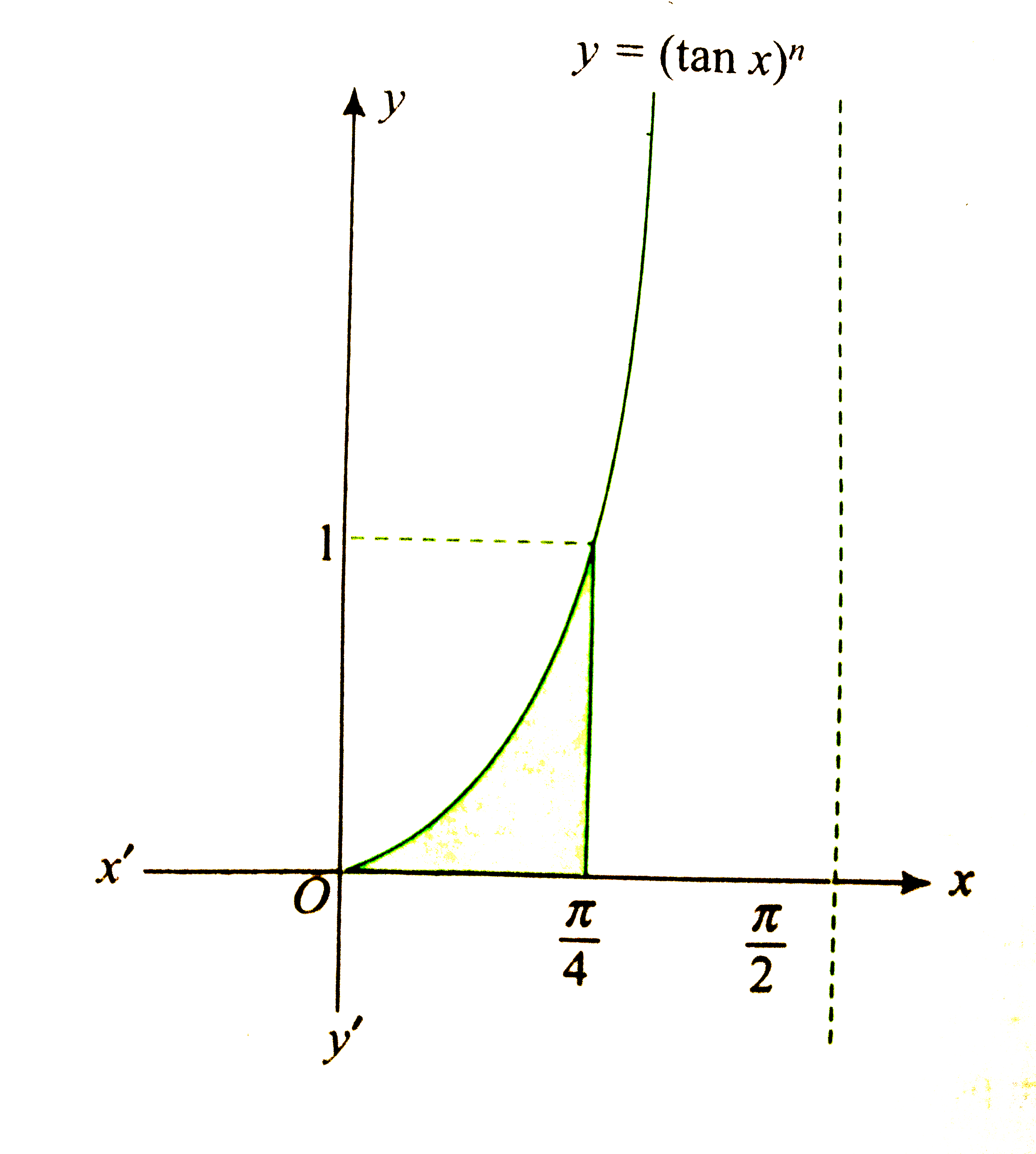
`"Since "0lt tna x lt 1," when "0 lt x lt pi//4,` we have
`0lt (tan x)^(n+1) lt (tan x)^(n)" for each "n in N`
`rArr" "int_(0)^(pi//4)(tan x)^(n+1) dx lt int_(0)^(pi//4) (tan x)^(n) dx`
`rArr" "A_(n+1)ltA_(n)`
`"Now, for "ngt2`,
`A_(n)+A_(n+2)=int_(0)^(pi//4)[(tan x)^(n)+(tan x)^(n+2)]dx`
`=int_(0)^(pi//4)(tan x)^(n)(1+ tan^(2)x) dx`
`=int_(0)^(pi//4)(tan x)^(n) (sec^(2)x) dx`
`=[(1)/((n+1))(tan x)^(n+1)]_(0)^(pi//4)`
`[because int [f(x)]^(n)f'(x)dx=([f(x)]^(n+1))/(n+1)]`
`=(1)/((n+1))(1-0)`
`"Since "A_(n+2)ltA_(n+1)ltA_(n),` we get
`A_(n)+A_(n+2)lt2A_(n)`
`rArr" "(1)/(n+1)lt2A_(n)rArr(1)/(2n+2)ltA_(n)" (1)"`
`"Also for "ngt2, A_(n)+A_(n)ltA_(n)+A_(n-2)=(1)/(n-1)`
`"or "2A_(n)lt(1)/(n-1)`
`"or "A_(n)lt(1)/(2n-2)" (2)"`
`"Combining (1) and (2), we get "(1)/(2n+2)ltA_(n)lt(1)/(2n-2).`