Home
Class 12
MATHS
Consider two regions R(1):"points P ar...

Consider two regions
`R_(1):"points P are nearer to (1,0) than to "x=-1.`
`R_(2): "Points P are nearer to (0,0) than to (8,0)"` Find the area of the region common to `R_(1) and R_(2).`

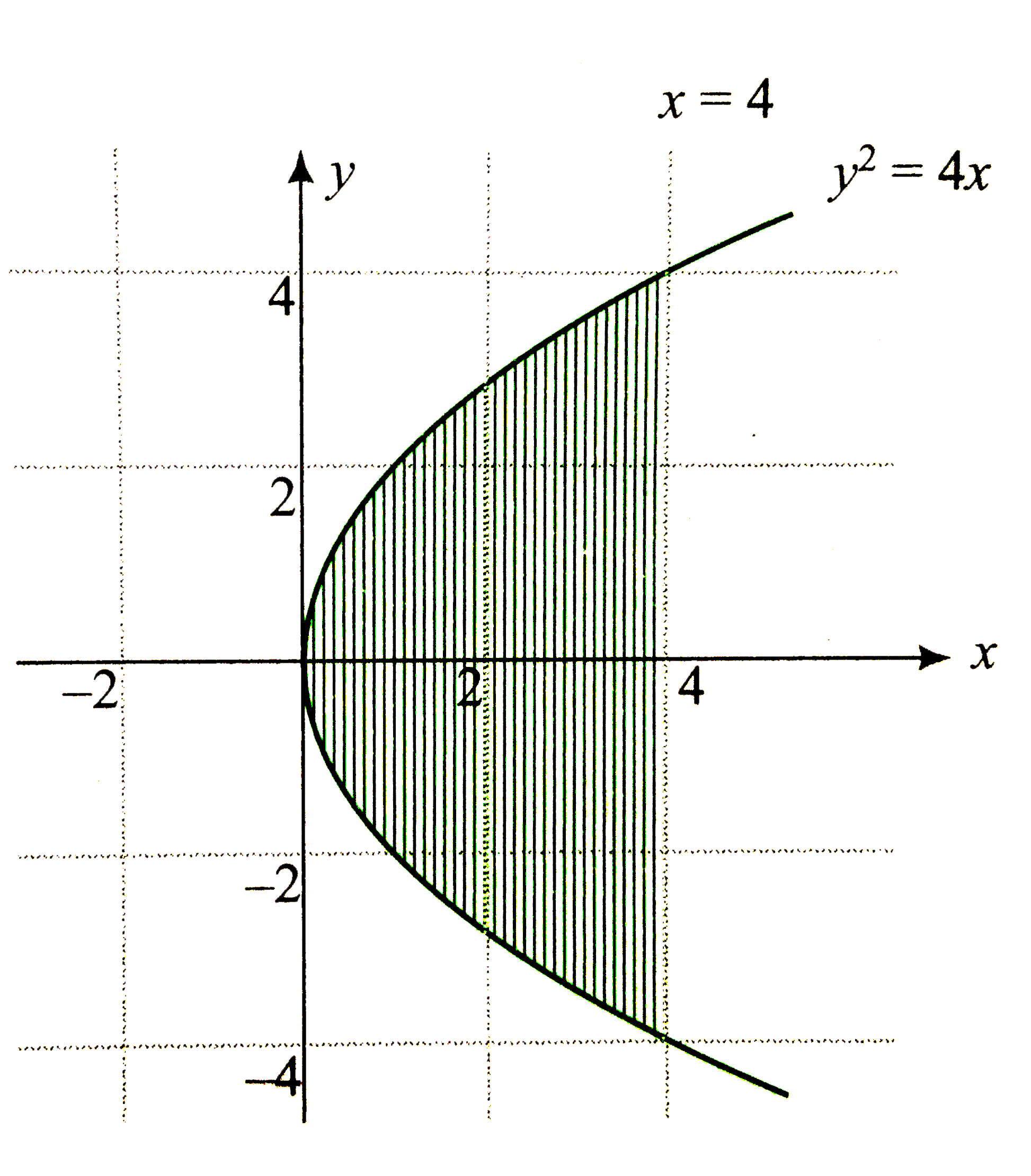
Text Solution

Verified by Experts

The correct Answer is:
`(64)/(3)` sq. units
`R_(1) :` points P(x,y) are nearer to (1,0) than to x=-1
`therefore" "sqrt((x-1)^(2)+y^(2))lt|x+1|`
`rArr" "y^(2)lt4x`
`rArr" point P lie inside parabola "y^(2)=4x`
`R_(2) :` Points P(x,y) are nearer to (0,0) than to (8,0)
`therefore" "|x|lt|x-8|`
`rArr" "x^(2)ltx^(2)-16x+64`
`rArr" "xlt4`
`rArr" "`point P lie to the left side of line x=4
The area of common region of `R_(1) and R_(2)` is area bounded by x=4 and `y^(2)=4x.`

`therefore" Required area "=2overset(4)underset(0)int(4-(y^(2))/(4))dy` (Integrating along x-axis)
`=2[4y-(y^(3))/(12)]_(0)^(4)`
`=2[16-(64)/(12)]`
`(64)/(3)` sq. units
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE|Exercise Exercise (Single)|40 Videos

  • AREA

    CENGAGE|Exercise Exercise (Multiple)|10 Videos

  • AREA

    CENGAGE|Exercise Exercise 9.2|14 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE|Exercise Subjective Type|2 Videos

  • AREA UNDER CURVES

    CENGAGE|Exercise Question Bank|10 Videos

Similar Questions

Explore conceptually related problems

The vertices of trianglePQR are P(0,-4),Q(3,1) and R(-8,1) Find the area of triangleMPN .

The vertices of trianglePQR are P(0,-4),Q(3,1) and R(-8,1) Find the area of trianglePQR .

Plot the region in the first quadrant in which points are nearer to the origin than to the line x=3.

The vertices of trianglePQR are P(0,-4),Q(3,1) and R(-8,1) Find the coordinates of N, the mid-point of QR.

Find the area of the triangle formed by the points P(-1.5, 3), Q(6, -2), and R(-3, 4) .

The vertices of trianglePQR are P(0,-4),Q(3,1) and R(-8,1) Find the coordinates of M , the mid-point of QP.

A point R with x-coordinate 4 lies on the line segment joining the points P(2,-3,4) and Q(8,0,10) . Find the coordinates of the point R.

In R^(3) , consider the planes P_(1):y=0 and P_(2),x+z=1. Let P_(3) be a plane, different from P_(1) and P_(2) which passes through the intersection of P_(1) and P_(2) , If the distance of the point (0,1,0) from P_(3) is 1 and the distance of a point (alpha,beta,gamma) from P_(3) is 2, then which of the following relation(s) is/are true?

Normals of parabola y^2=4 x at P and Q meet at R(x_2, 0) and tangents at P and Q mect-at T(x_1, 0) . If x_2=3 , then find the area of quadrilateral P T Q R .

Given that P(3,1),Q(6. 5), and R(x , y) are three points such that the angle P Q R is a right angle and the area of R Q P is 7, find the number of such points Rdot