a.
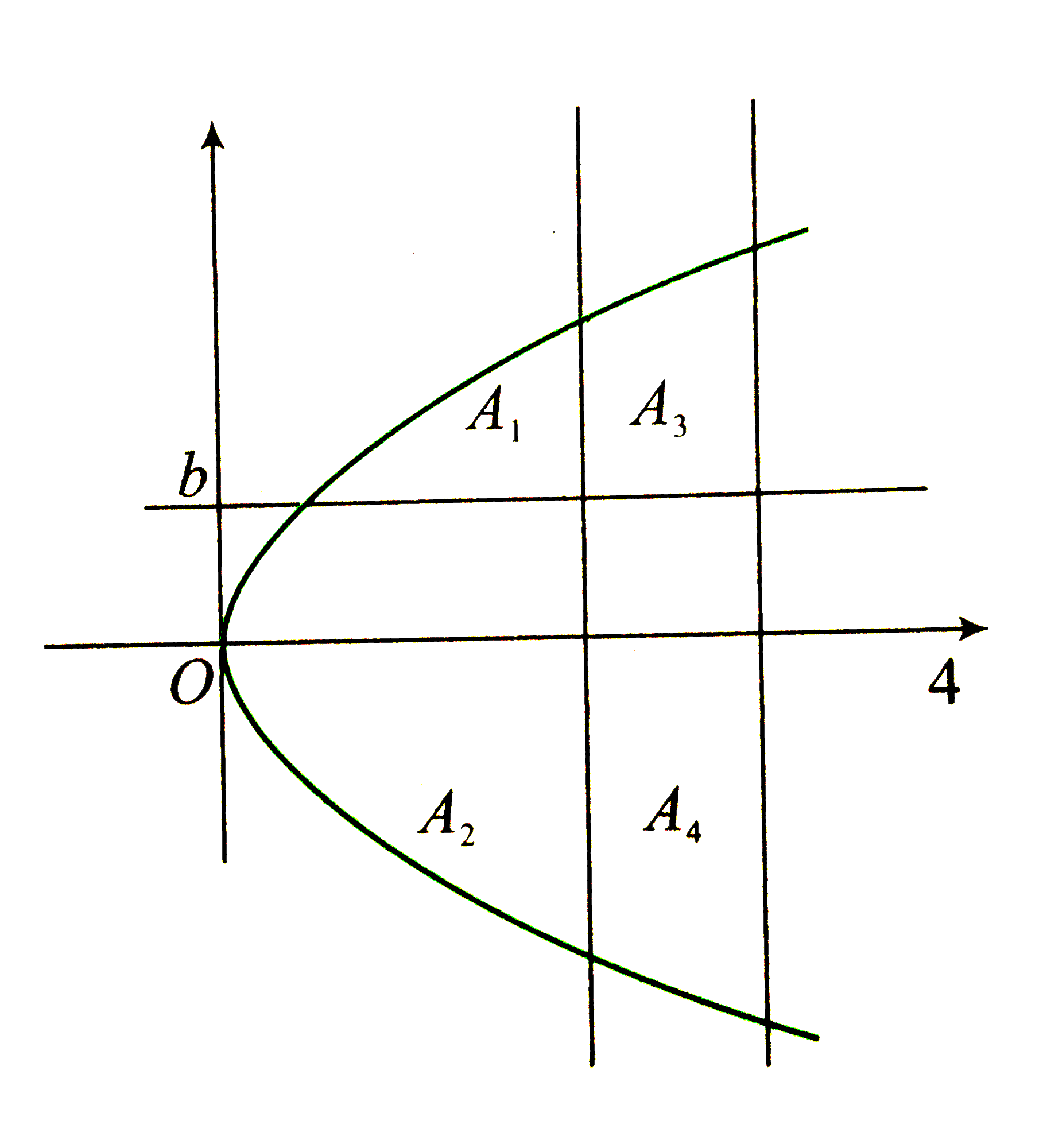
`"Total area "=2overset(4)underset(0)intsqrt(x)dx=(32)/(3)`
`"Area of each part "=8//3`
`A_(3)=A_(4)rArroverset(4)underset(a)int(sqrt(x)-b)dx=overset(4)underset(a)int(b+sqrt(x))dx=(8)/(3)`
`therefore" "b=0`
`therefore" "overset(4)underset(a)intsqrt(x)dx=(8)/(3)`
`therefore" "a^(3)=16`
b. `f(x)={{:(x^((1)/(log_(e)x))",",xne1),(e",",x=1):}={{:(x^((1)/(log_(e)x))",",xne1),(e",",x=1):}=e`
Hence required area bound by `y=f(x) and y=|x-e|" is "e^(2)`
c.
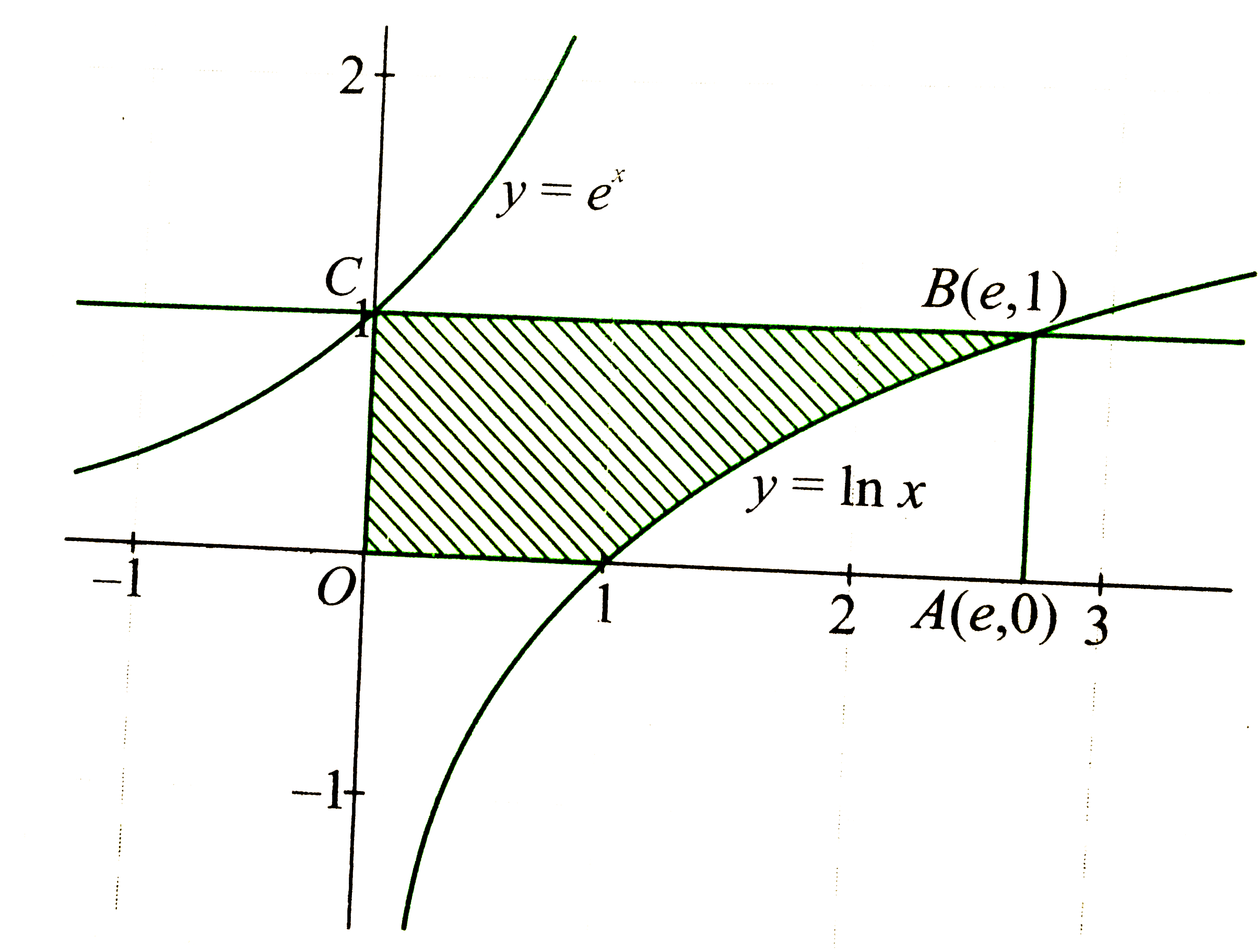
Area = Area of rectangle `OABC-overset(e)underset(1)" In "xdx`
`=e-1` sq. units.
d. Solving `2 cos x =3 tan x we get, 2-2 sin^(2)x =3 sin x`
`rArr" "sin x=(1)/(2)rArrx=(pi)/(6)`
`"Required area "=overset(pi//6)underset(0)int(2cos x- 3 tan x)dx`
`=(2 sin x -3" In "sec x)_(0)^(pi//6)`
`=1+(3)/(2)log_(e)3-3log_(e)2`