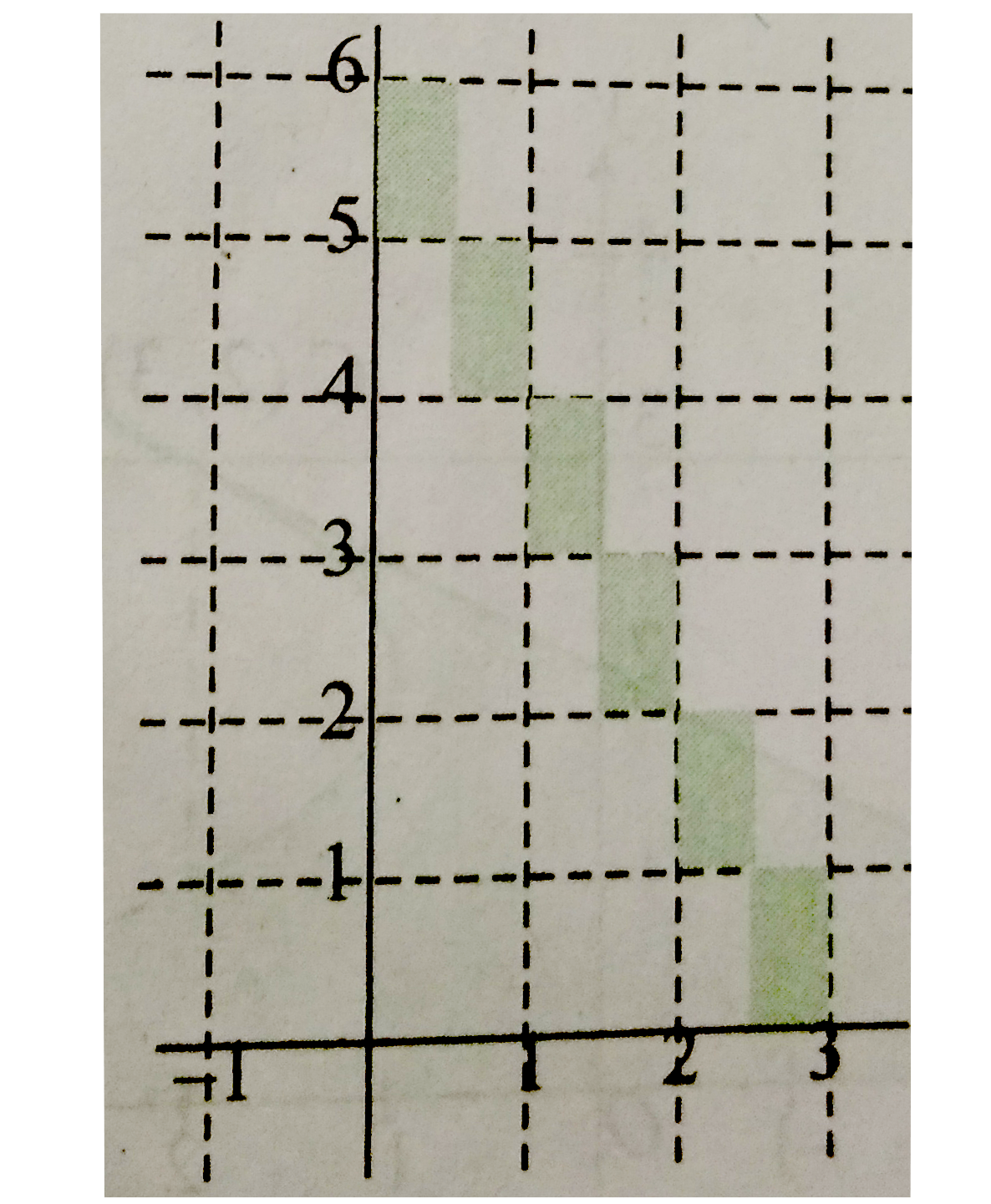
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-AREA-Exercise (Numerical)
- The area enclosed by the curve C:y=xsqrt(9-x^(2))(xge0) and the x-axis...
Text Solution
|
- Let S be the area bounded by the curve y=sinx(0lt=xlt=pi) and the x-ax...
Text Solution
|
- Let C be a curve passing through M(2,2) such that the slope of the tan...
Text Solution
|
- The area enclosed by f(x)=12+ax-x^(2) coordinates axes and the coordin...
Text Solution
|
- If the area bounded by the curve f(x)=x^(1//3)(x-1) and the x-axis is ...
Text Solution
|
- If the area bounded by the curve y=x^2+1 and the tangents to it drawn ...
Text Solution
|
- Find the area enclosed by the curves y= sqrtx and x= -sqrty and the c...
Text Solution
|
- The value of a(agt0) for which the area bounded by the curves y=(x)/(6...
Text Solution
|
- Area bounded by the curve [|x|] + [|y|] = 3, where [.] denotes the gre...
Text Solution
|
- The area bounded by the curves y=x(x-3)^2a n dy=x is (in sq. units)
Text Solution
|
- If the area of the region {(x , y):0lt=ylt=x^2+1,0lt=ylt=x+1,0lt=xlt=2...
Text Solution
|
- If S is the sum of possible values of c for which the area of the figu...
Text Solution
|
- If A is the area bounded by the curves y=sqrt(1-x^2) and y=x^3-x , the...
Text Solution
|
- Consider the two curves C(1):y=1+cos x and C(2): y=1 + cos (x-alpha)" ...
Text Solution
|
- If ' a^(prime)(a >0) is the value of parameter for each of which the a...
Text Solution
|
- If S is the sum of cubes of possible value of c for which the area of ...
Text Solution
|