Home
Class 12
MATHS
In a DeltaABC, A = (2,3) and medians thr...

In a `DeltaABC, A = (2,3)` and medians through B and C have equations `x +y - 1 = 0` and `2y - 1 = 0`
Equation of median through A is

A

`x +y = 4`

B

`5x - 3y = 1`

C

`5x +3y = 1`

D

`5x = 3y`

Text Solution

Verified by Experts

The correct Answer is:
B

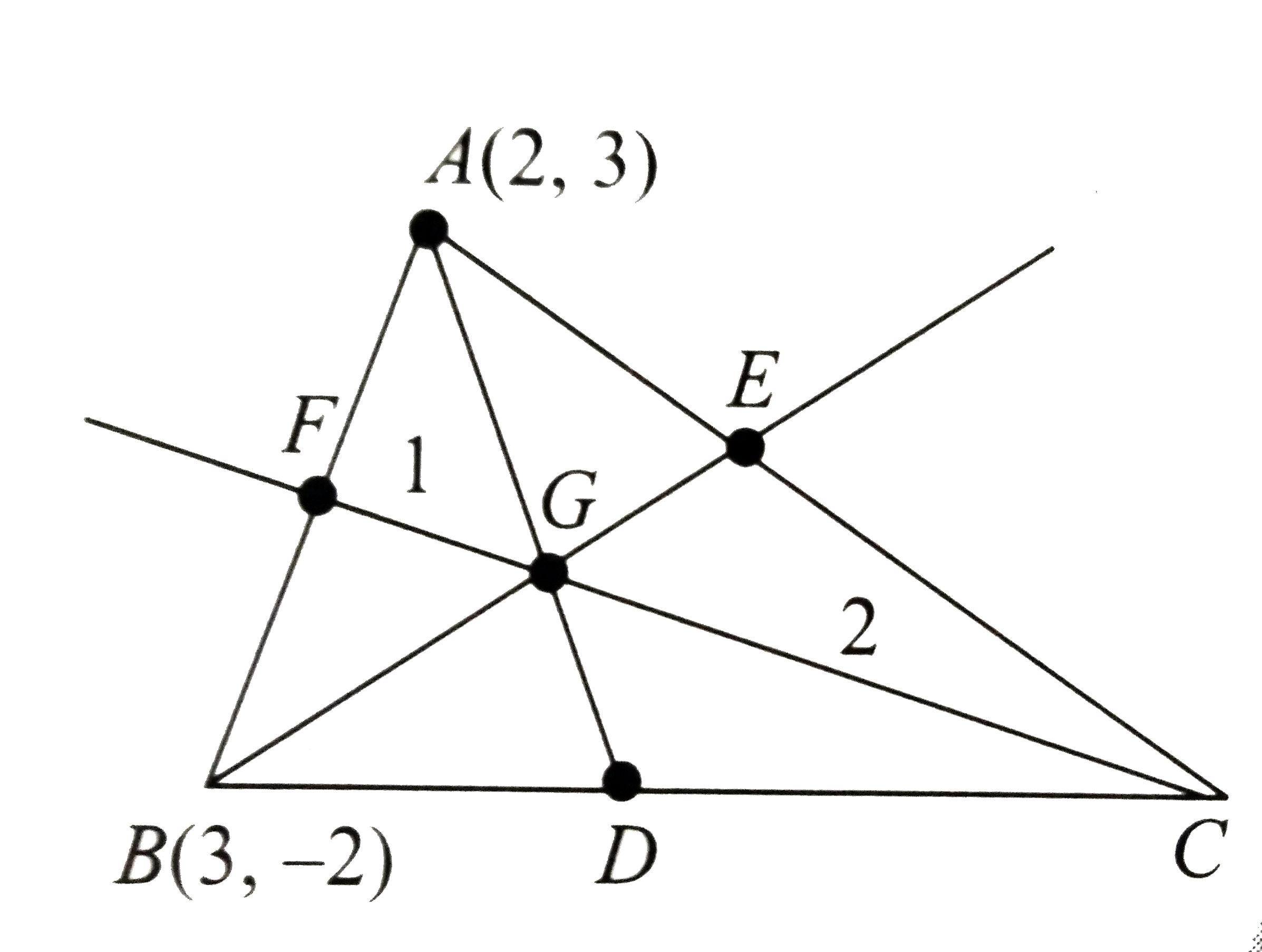
Centroid is the point of intersection of `x +y -1 = 0, 2y -1 = 0` or `D ((1)/(2),(1)/(2))`
Slope of AD is `(3-(1)/(2))/(2-(1)/(2)) =(5)/(3)`
`:.` Equation of AD is `y - 3 = (5)/(3) (x-2)` or `5x - 3y - 1 = 0`
A point of `CF: 2y - 1 = 0` is `(alpha, (1)/(2))`
Let this be the midpoint of AB.
`:.` B is `(2alpha -2,-2)` which lies on median `BE: x +y - 1 = 0`
`:. 2alpha -2-2-1 = 0 :. alpha =(5)/(2)`
`:. B (3,-2)`
G divides CF in 2:1
`:. C = ((-7)/(2),(1)/(2))`
`:.` Equation of BC is `(y+2)/((1)/(2)+2) = (x-3)/((-7)/(2)-3)`
or `(y+2)/(5) =(x-3)/(-13)`
or `5x +13y +11 = 0`
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • STATISTICS

    CENGAGE|Exercise JEE Previous Year|10 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise JEE Advanced Previous Year|4 Videos

Similar Questions

Explore conceptually related problems

A straight line passes through (1,2) and has the equation y-2x-k =0 . Find k.

The vertex A of DeltaABC is (3,-1). The equation of median BE and angle bisector CF are x-4y+10=0 and 6x+10y-59=0, respectively. Equation of AC is

The base B C of a A B C is bisected at the point (p ,q) & the equation to the side A B&A C are p x+q y=1 & q x+p y=1 . The equation of the median through A is: (a) (p-2q)x+(q-2p)y+1=0 (b) (p+q)(x+y)-2=0 (c) (2p q-1)(p x+q y-1)=(p^2+q^2-1)(q x+p y-1) (d)none of these

In a triangle ABC, AB is parallel to y-axis, BC is parallel to x-axis, centroid is at (2, 1), If median through C is x-y=1 , then the slope of median through A is

The vertices of Delta PQR " are " P (2, 1) , Q (-2, 3) " and " R (4, 5) . Find equation of the median through the vertex R.

Find the equation of the plane through the intersection of the planes 2x - 3y + z - = 0 and x - y + z + 1 = 0 and perpendicular to the plane x + 2y - 3z + 6 = 0.

Find the equation of the plane containing the line of intersection of the planes x + y + z - 6 = 0 and 2x + 3y + 4z + 5 = 0 and passing through the point (1,1,1)

Find the equation of the line passing through the point of intersection of the lines 4x + 7y - 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.

A curve C passes through (2,0) and the slope at (x , y) as ((x+1)^2+(y-3))/(x+1)dot Find the equation of the curve.

Find the equation of a line through (-1,3) perpendicular to the line 2x + 3y + 1 = 0.