A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
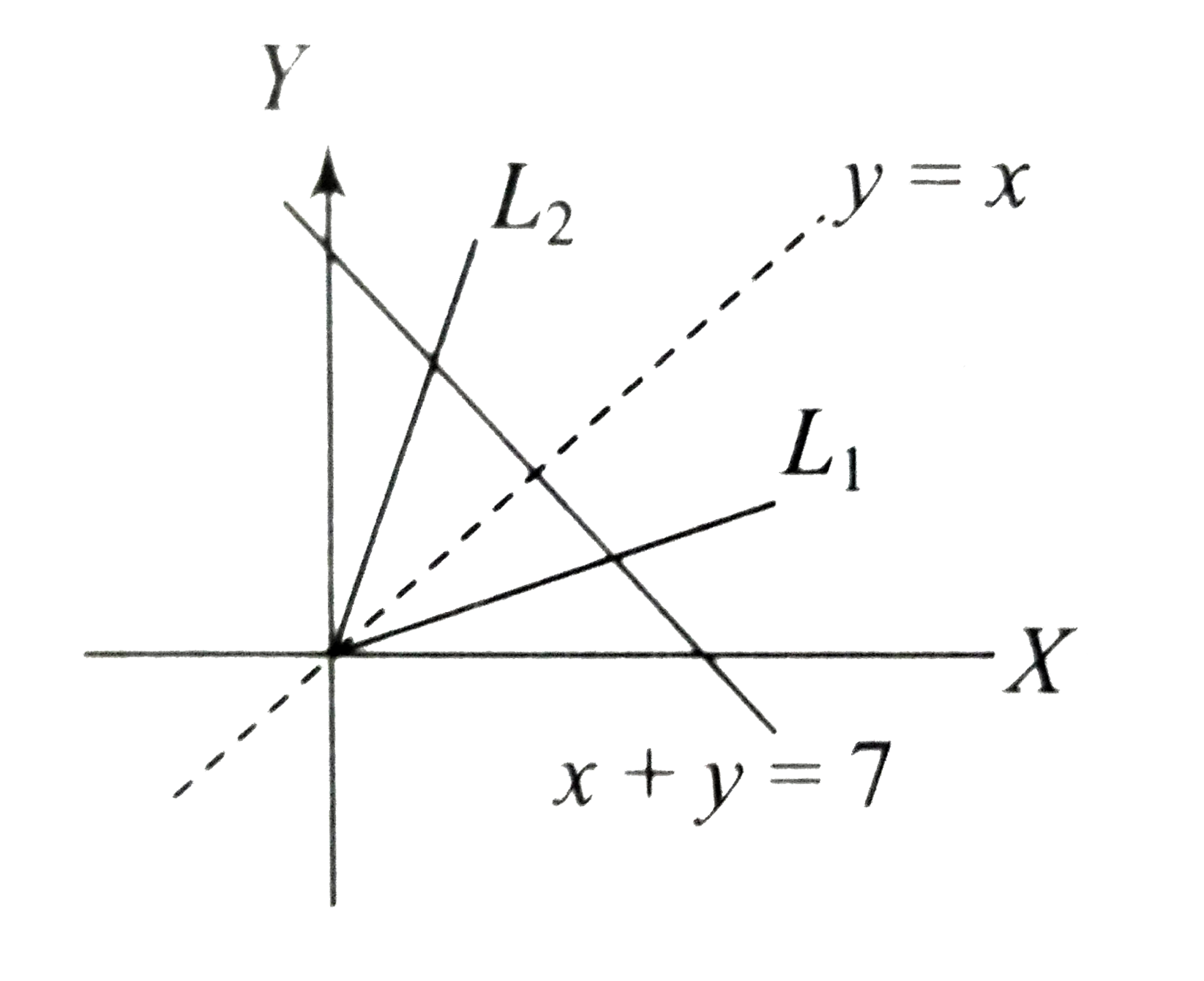
- x+y=7 and a x^2+2h x y+a y^2=0,(a!=0) , are three real distinct lines ...
Text Solution
|
- x+y=7 and a x^2+2h x y+a y^2=0,(a!=0) , are three real distinct line...
Text Solution
|
- The straight lines x +y=0, 5x + y= 4 and x+5y=4 form (A) an isosceles ...
Text Solution
|
- The pair of straight lines x^(2)-4xy+y^(2)=0 together with the line x+...
Text Solution
|
- The triangle formed by the pair of lines x^(2)-4y^(2)=0 and the line x...
Text Solution
|
- The straight lines x+y=0, 3x+y-4=0 and x+3y-4=0 form a triangle which ...
Text Solution
|
- Show that the straight lines x^2+4xy+y^2=0 and the line x-y=4 form a...
Text Solution
|
- Show that the straight line x^2-4xy+y^2=0 and x + y = 3 form an equila...
Text Solution
|
- x+y=7 and a x^2+2h x y+a y^2=0,(a!=0) , are three real distinct line...
Text Solution
|