A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PARABOLA
CENGAGE|Exercise Multiple Correct Answers Type|10 VideosPARABOLA
CENGAGE|Exercise Comprehension Type|1 VideosPARABOLA
CENGAGE|Exercise JEE Advenced Single Answer Type|18 VideosPAIR OF STRAIGHT LINES
CENGAGE|Exercise Exercise (Numerical)|5 VideosPERMUTATION AND COMBINATION
CENGAGE|Exercise Question Bank|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-PARABOLA-Single Correct Answer Type
- Sum of slopes of common tangent to y = (x^(2))/(4) - 3x +10 and y = 2 ...
Text Solution
|
- The slope of normal to be parabola y = (x^(2))/(4) -2 drawn through th...
Text Solution
|
- The tangent and normal at the point P(4,4) to the parabola, y^(2) = 4x...
Text Solution
|
- The point on the parabola y^(2) = 8x at which the normal is inclined a...
Text Solution
|
- about to only mathematics
Text Solution
|
- From an external point P, a pair of tangents is drawn to the parabola ...
Text Solution
|
- A variable parabola y^(2) = 4ax, a (where a ne -(1)/(4)) being the par...
Text Solution
|
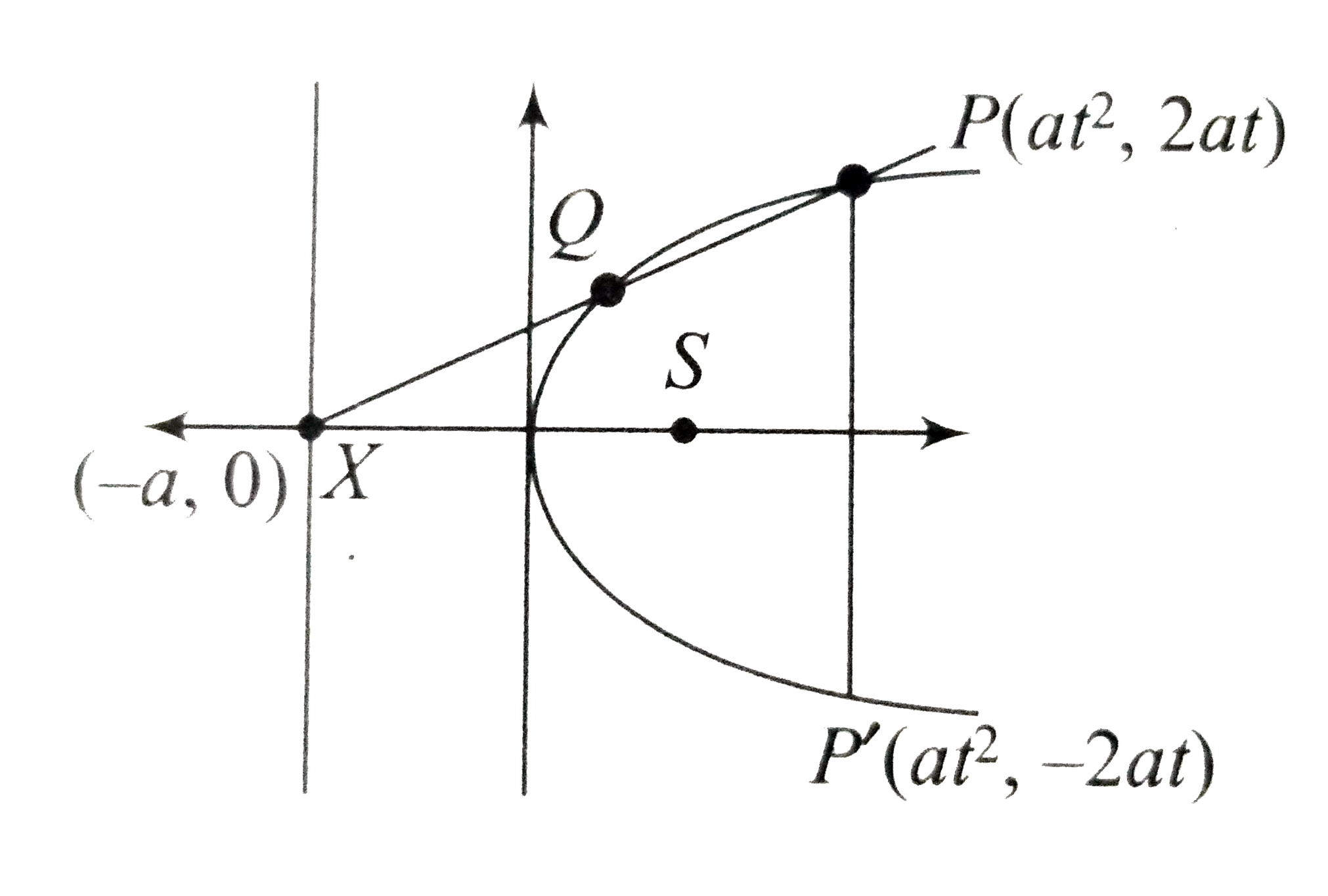
- If X is the foot of the directrix on the a parabola. PP' is a double o...
Text Solution
|
- Let PQ be the latus rectum of the parabola y^2 = 4x with vetex A. Mini...
Text Solution
|
- Through the vertex O of the parabola y^(2) = 4ax, a perpendicular is d...
Text Solution
|
- Tangents PQ and PR are drawn to the parabola y^(2) = 20(x+5) and y^(2)...
Text Solution
|
- The locus of centroid of triangle formed by a tangent to the parabola ...
Text Solution
|
- PC is the normal at P to the parabola y^2=4ax, C being on the axis. CP...
Text Solution
|
- If three parabols touch all the lines x = 0, y = 0 and x +y =2, then m...
Text Solution
|
- If 2x +3y = alpha, x -y = beta and kx +15y = r are 3 concurrent normal...
Text Solution
|
- Let (2,3) be the focus of a parabola and x + y = 0 and x-y= 0 be its t...
Text Solution
|
- In the following figure, AS = 4 and SP = 9. The value of SZ is
Text Solution
|
- TP and TQ are any two tangents to a parabola and the tangent at a th...
Text Solution
|
- The distance of two points P and Q on the parabola y^(2) = 4ax from th...
Text Solution
|
- A parabola having directrix x +y +2 =0 touches a line 2x +y -5 = 0 at ...
Text Solution
|