Home
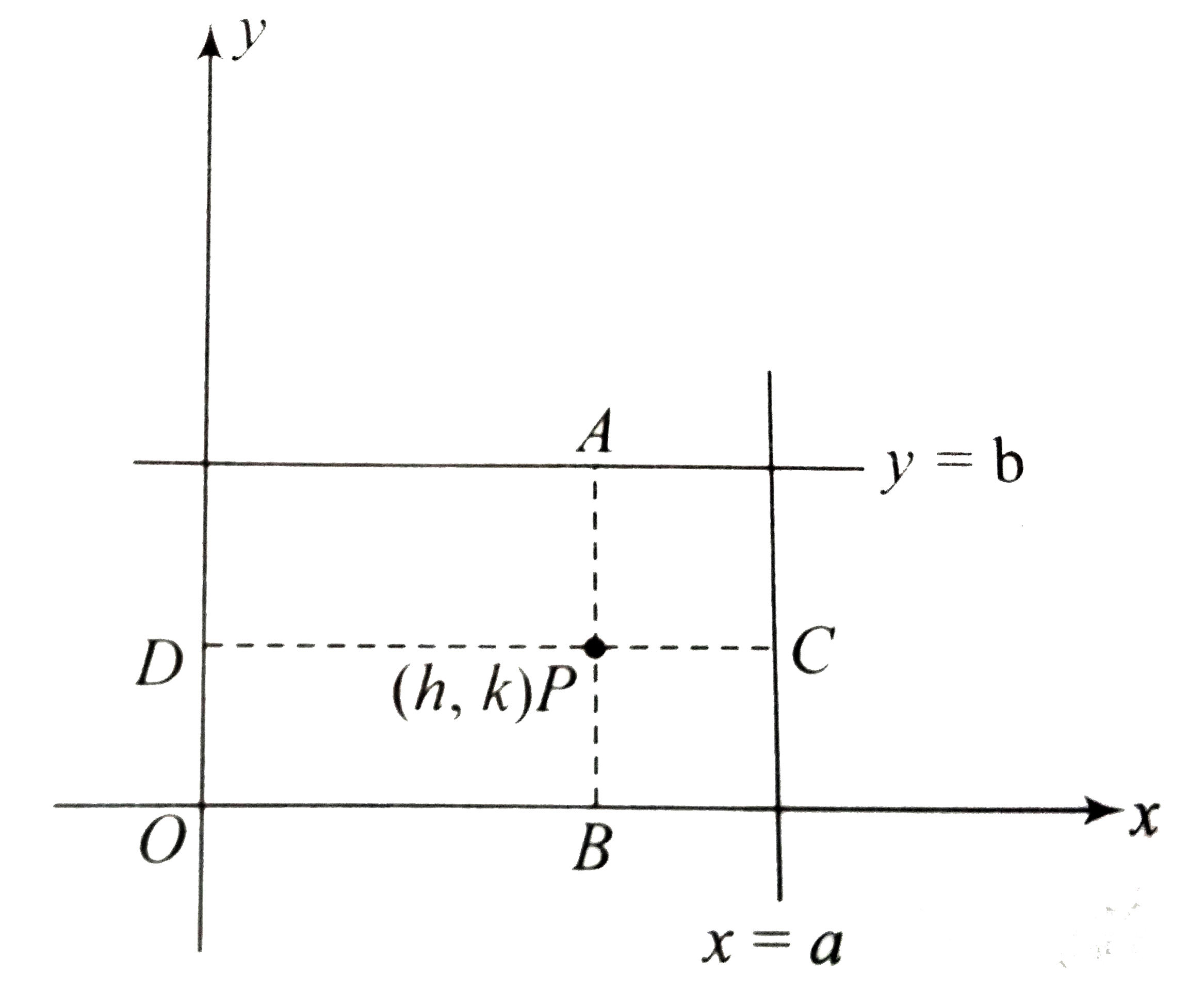
Class 12
MATHS
A point moves such that the sum of the s...

A point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:

A

a circle

B

an ellipse

C

a hyperbola

D

a pair of lines

Text Solution

Verified by Experts

The correct Answer is:
C, D
Let the two sides of the rectangle lie along x-axis and y-axis.

Let point P be (h,k)
Given that
`(PA)^(2) + (PB)^(2) = 2 (PC^(2)+PD^(2))`
`rArrk^(2) - (k-b)6(2) = 2(h^(2) + (a-h)^(2))`
`rArr 2k^(2) - 2kb + b^(2) = 4h^(2) - 4ah + 2a^(2)`
Replacing h by x and k by y
`rArr 2y^(2) - 2by + b^(2) = 4x^(2) - 4ax + 2a^(2)`
or `2(y^(2)-by) + b^(2) = 4(x^(2)-ax) + 2a^(2)`
or `4(x-(a)/(2))^(2) - 2(y-(b)/(2))^(2) = (b^(2))/(2) -a^(2)`
Hence it is a hyperbola if `(b^(2))/(2) -a^(2) ne 0`
or pair of lines if `(b^(2))/(2) -a^(@) =0`
Promotional Banner

Similar Questions

Explore conceptually related problems

Prove that the sum of the squares of the squares of tha diagonals of a parallelogram is equal to tha sum of the squares of its sides.

A point moves such that the sum of the square of its distances from two fixed straight lines intersecting at angle 2alpha is a constant. Prove that the locus of points is an ellipse

In triangle ABC, a = 4 and b = c = 2 sqrt(2) . A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals

Prove that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.

The locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an (a)circle (b) straight line (c) ellipse (d) none of these

Prove that in a right triangle, the square of the hypotenure is equal to the sum of the squares of the others two sides.

Find the locus of a point such that the sum of its distance from the points (2, 2) and (2,-2) is 6.

Find the equation of the locus of a point such that the sum of the squares of the distance from the points (3, 5), (1, -1) is equal to 20.