Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-CIRCLE -Exercise 4.5
- How the following pair of circles are situated in the plane ? Als, fi...
Text Solution
|
- If the circles of same radius a and centers at (2, 3) and 5, 6) cut or...
Text Solution
|
- Circles of radius 5 units intersects the circle (x-1)^(2)+(x-2)^(2)=9...
Text Solution
|
- about to only mathematics
Text Solution
|
- Let two parallel lines L1 and L2 with positive slope are tangent to th...
Text Solution
|
- about to only mathematics
Text Solution
|
- The equation of a circle is x^2+y^2=4. Find the center of the smallest...
Text Solution
|
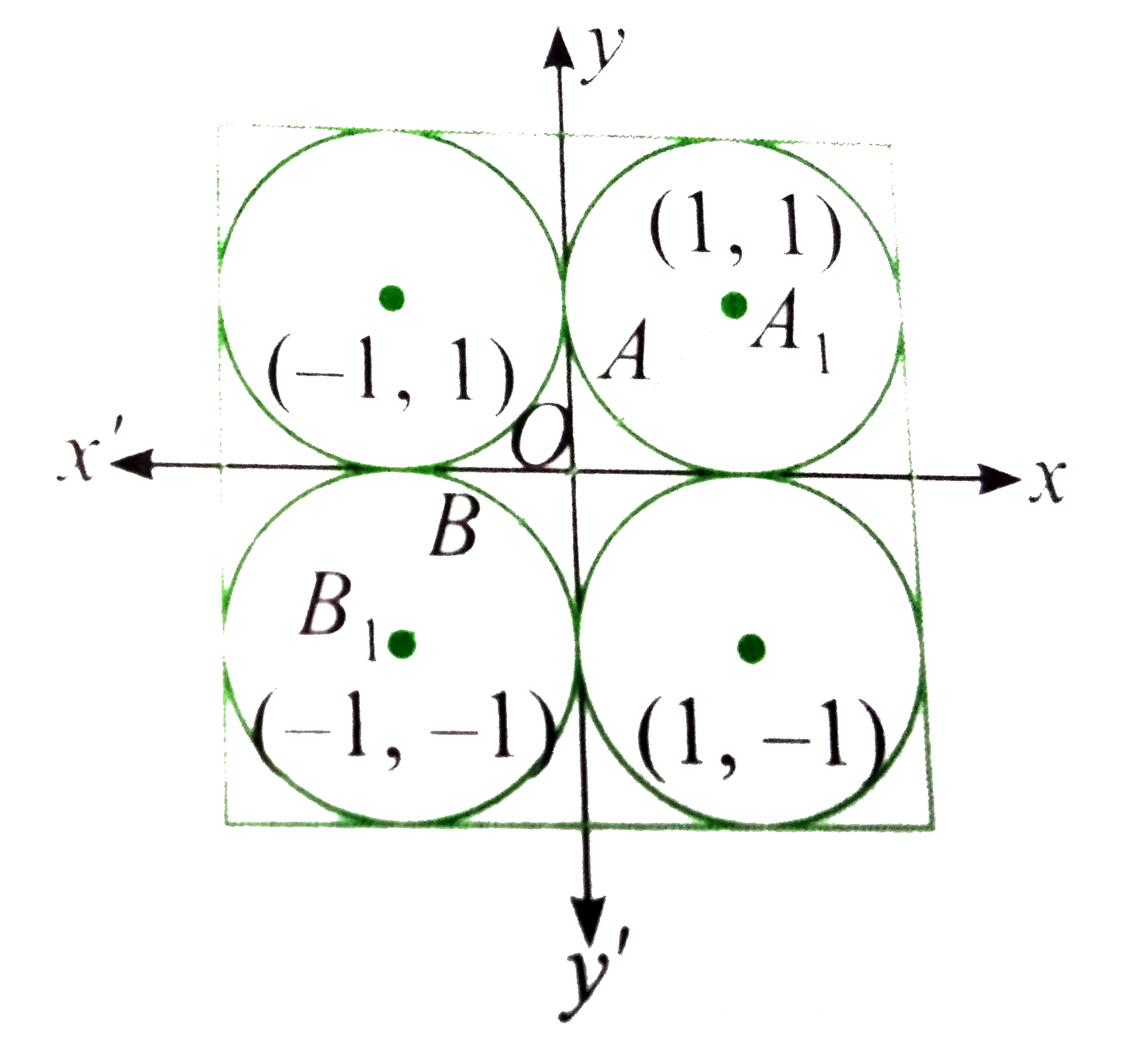
- Consider four circles (x+-1)^2+(y+-1)^2=1 . Find the equation of the s...
Text Solution
|
- Find the equation of the circle whose radius is 3 and which touches ...
Text Solution
|
- Two circles with radii aa n db touch each other externally such that t...
Text Solution
|
- If the radii of the circles (x-1)^2+(y-2)^2=1 and (x-7)^2+(y-10)^2=4 a...
Text Solution
|
- about to only mathematics
Text Solution
|