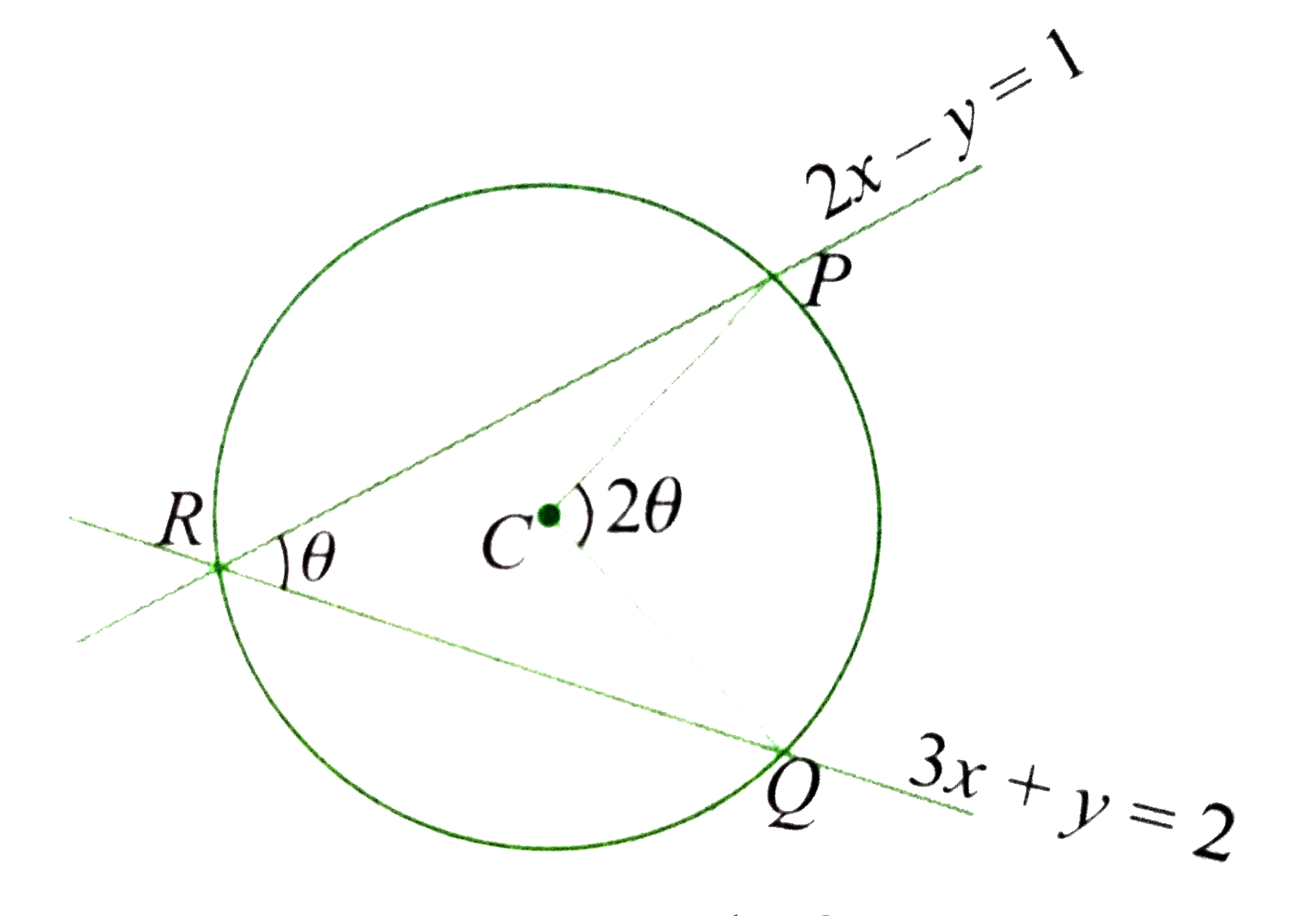
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-CIRCLE -Exercise (Single)
- If a circle of radius r is touching the lines x^2-4x y+y^2=0 in the fi...
Text Solution
|
- The locus of the midpoints of the chords of the circle x^2+y^2-a x-b y...
Text Solution
|
- Any circle through the point of intersection of the lines x+sqrt(3)y=1...
Text Solution
|
- If the pair of straight lines x ysqrt(3)-x^2=0 is tangent to the circl...
Text Solution
|
- The condition that the chord xcosalpha+ysinalpha=p=0 of x^2+y^2-a^2=0 ...
Text Solution
|
- The centers of a set of circles, each of radius 3, lie on the circle x...
Text Solution
|
- The equation of the locus of the middle point of a chord of the circle...
Text Solution
|
- The angle between the pair of tangents drawn from a point P to the cir...
Text Solution
|
- If two distinct chords, drawn from the point (p, q) on the circle x^2+...
Text Solution
|
- If one of the diameters of the circle x^2+y^2-2 x-6 y+6 =0 is a chord ...
Text Solution
|
- Through the point P(3,4) a pair of perpendicular lines are dranw which...
Text Solution
|
- A circle with center (a , b) passes through the origin. The equation...
Text Solution
|
- A straight line with slope 2 and y-intercept 5 touches the circle x^2+...
Text Solution
|
- The locus of the point from which the lengths of the tangents to the ...
Text Solution
|
- about to only mathematics
Text Solution
|
- A line meets the coordinate axes at A and B . A circle is circumscribe...
Text Solution
|
- The range of values of alpha for which the line 2y=gx+alpha is a norma...
Text Solution
|
- The equation of the tangent to the circle x^2+y^2=a^2, which makes a t...
Text Solution
|
- From an arbitrary point P on the circle x^2+y^2=9 , tangents are drawn...
Text Solution
|
- about to only mathematics
Text Solution
|