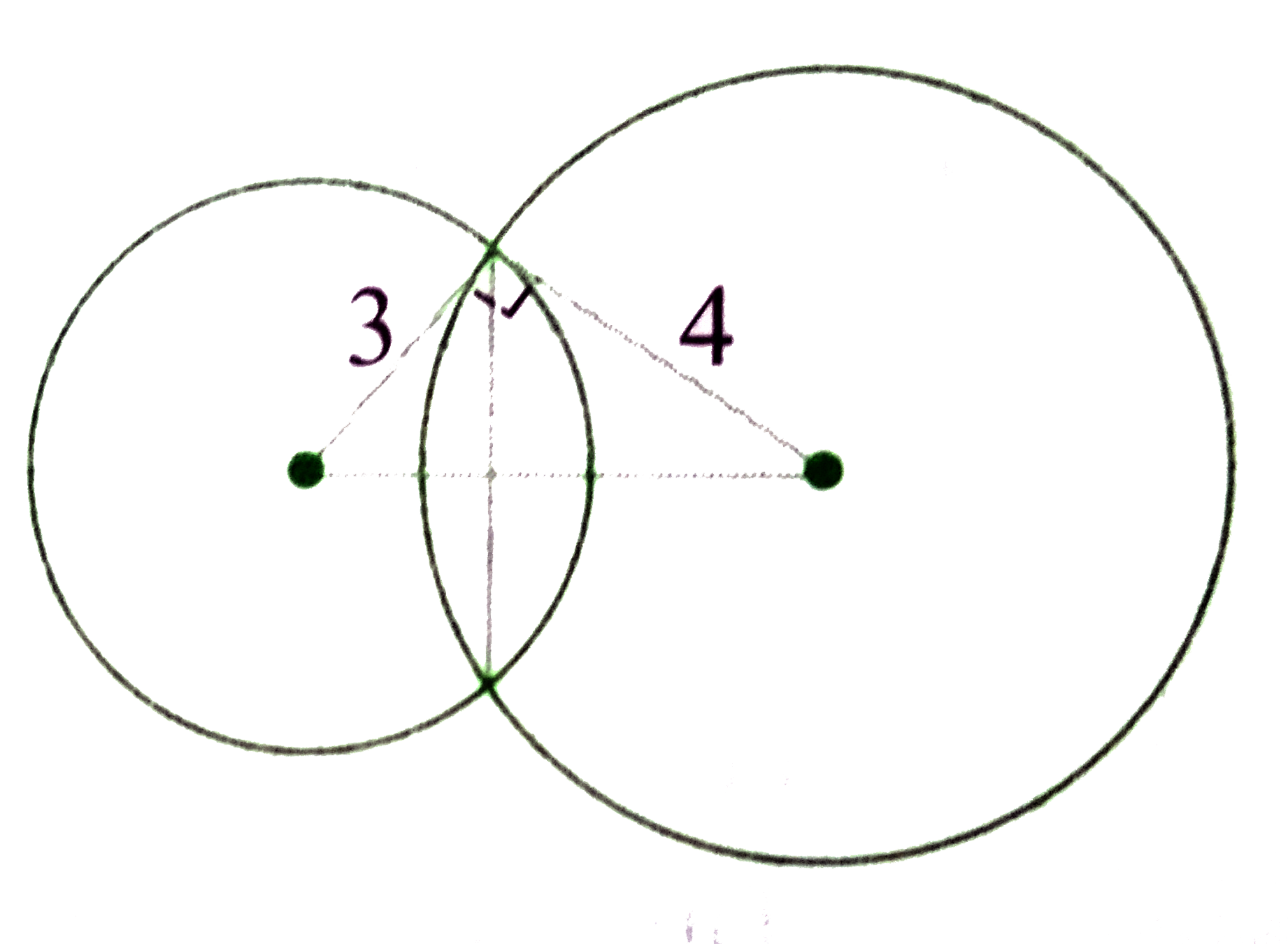
a. Let the length of the common chord be 2a. Then,
`sqrt(9-a^(2))+sqrt(16-a^(2))=5`
or `sqrt(16-a^(2))=5-sqrt(9-a^(2))`
or `16-a^(2)=25+9-a^(2)-10sqrt(9-a^(2))`
or `10sqrt(9-a^(2))=18`
or `100(9-a^(2))=324`
i.e., `100a^(2) =576`
or `a= sqrt((576)/(100))=(24)/(10)`
`:. 2a=(24)/(5)=(k)/(5) `or `=24`
b. The equation of common chord is `6x+4y+p+q=0`.
The common chord passes through the center `( -2,-6)` of the circle `x^(2)+y^(2)+4x+12y+p=0` . Therefore,
`p+q=36`
c. The equation of the circle is `2x^(2)+2y^(2)-2sqrt(2) x-y=0`
Let `( alpha , 0)` be the midpoint of a chord . Then the equation of the chord is
`2 alpha x -sqrt(2) (x+alpha) -(1)/(2) (y+0)= 2 alpha^(2)-2 sqrt(2) alpha`
Since it passes through the point `( sqrt(2) , 1//2)` , we have
`2 sqrt(2) alpha - sqrt (2) ( sqrt(2)+alpha )-(1)/(4)= 2 alpha^(2)-2 sqrt(2) alpha `
i.e., `8 alpha^(2)-12 sqrt(2) alpha + 9 =0`
i.e., `( 2 sqrt(2) alpha -3)^(2)=0`
i.e., ` alpha = (3)/(2 sqrt(2))`
Therefore, the number of chords is 1.
d. Midpoint of AB `-= (1,4)`.
The equation perpendicular bisector of AB is `x=1`
A diameter of the circle is `4y= x+7`
Therefore, the center of the circle is `(1,2)`
Hence, the sides of the rectangle are 8 and 4. Therefore, area `=32`
