Home
Class 12
MATHS
The two circles x^2+y^2=ax and x^2+y^2=c...

The two circles `x^2+y^2=ax and x^2+y^2=c^2(c > 0)` touch each other if (1) `a=2c` (2) `|a|=2c` (3) `2|a|=c` (4) `|a|=c`

A

`|a| = 2c`

B

`2 |a| =c`

C

` | a| =c`

D

`a = 2c`

Text Solution

Verified by Experts

The correct Answer is:
3

The figure is self-explanatory, Clearly `c= |a|`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE|Exercise JEE Advanced (Single Correct Answer Type)|14 Videos

  • CIRCLE

    CENGAGE|Exercise MATRIX MATCH TYPE|6 Videos

  • CIRCLE

    CENGAGE|Exercise Exercise (Numerical)|18 Videos

  • BINOMIAL THEOREM

    CENGAGE|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE|Exercise Question Bank|16 Videos

Similar Questions

Explore conceptually related problems

If the circles x^2 + y^2 + 2ax + b = 0 and x^2+ y^2+ 2cx + b = 0 touch each other (a!=c)

The circle x^2 + y^2 - 4x + 6y + c = 0 touches x axis if

If the circles x^2+y^2-9=0 and x^2+y^2+2alpha x+2y+1=0 touch each other, then alpha is (a) -4/3 (b) 0 (c) 1 (d) 4/3

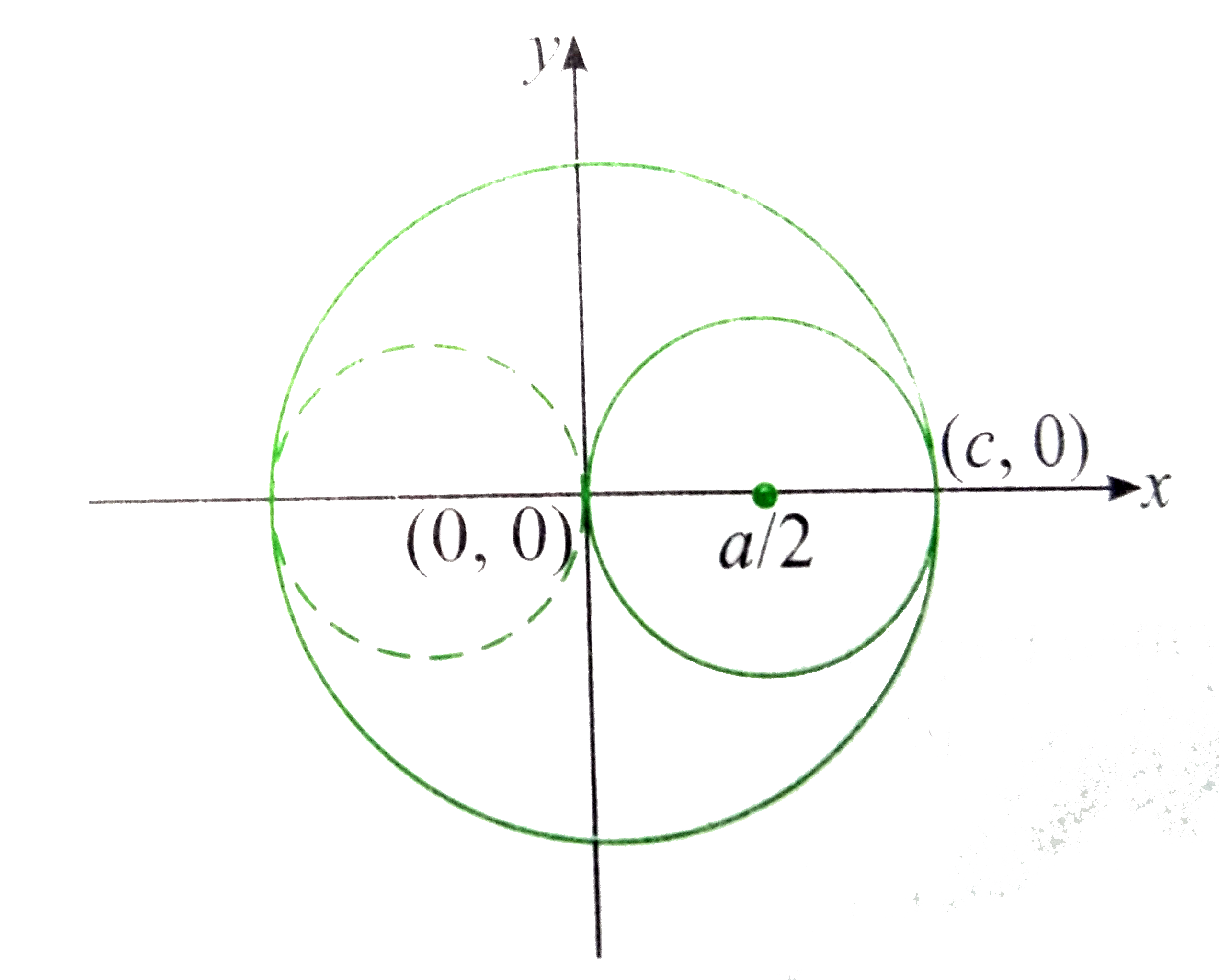
If two circles x^(2)+y^(2)+c^(2)=2ax and x^(2)+y^(2)+c^(2)-2by=0 touch each other externally , then prove that (1)/(a^(2))+(1)/(b^(2))=(1)/(c^(2))

Let the parabolas y=x(c-x)a n dy=x^2+a x+b touch each other at the point (1,0). Then (a) a+b+c=0 (b) a+b=2 (c) b-c=1 (d) a+c=-2

The curves 2x^(2) + 3y^(2) = 1 and cx^(2) + 4y^(2) = 1 cut each other orthogonally then the value of c is:

The two lines represented by 3a x^2+5x y+(a^2-2)y^2=0 are perpendicular to each other for (a)two values of a (b) a (c)for one value of a (d) for no values of a

Consider two curves C1:y^2=4x ; C2=x^2+y^2-6x+1=0 . Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other

If the radical axis of the circles x^2+y^2+2gx+2fy+c=0 and 2x^2+2y^2+3x+8y+2c=0 touches the circle x^2+y^2+2x+1=0 , show that either g=3/4 or f=2

Statement 1 :The circles x^2+y^2+2p x+r=0 and x^2+y^2+2q y+r=0 touch if 1/(p^2)+1/(q^2)=1/r dot Statement 2 : Two centers C_1a n dC_2 and radii r_1a n dr_2, respectively, touch each other if |r_1+-r_2|=c_1c_2dot